Asymptoteの練習 No.0005 テオドロスの螺線

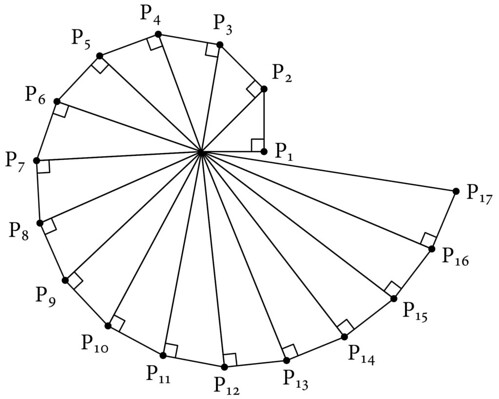
引き続き、繰り返し処理。テオドロスの螺線 (Spiral of Theodorus) を描いてみる。
三辺が$1$, $1$, $\sqrt2$の直角三角形から始めて、斜辺の上に高さ1の直角三角形を次から次へと作っていくことで、この図形は作られている。

伝説(？)によれば、テオドロスはルート2から始めて、自然数の平方根が整数になる場合を除いて無理数になることの証明をルート17まで行ったという。この螺線における直角三角形の斜辺がちょうど$\sqrt2$, $\sqrt3$, … , $\sqrt{17}$ となっていて、これ以上進めると三角形が重なってしまうので、ここで止めたのだろうという話を何処かで読んだ。

繰り返し以外のポイントとしては、線分$OP_{i}$を90度回転させて長さを1にしたものを線分$P_{i}P_{i+1}$とすることで、次の直角三角形を作るところ。AsymptoteはMetapostと同様に複素数としての演算が出来るが、それ以外にも、アフィン変換がサポートされている。今回は rotate という回転を行うオペレーターと、単位ベクトルを作る unit という関数を用いた。

/*
  Asymptoteの練習 No.0005
  繰り返し処理
  Spiral of Theodorus (テオドロスの螺線)
  t0005.asy
*/

size(6cm,0); // 出来上がりの図版のサイズを幅6センチに設定

int n=17;
pair pO=(0,0);
pair[] pA;

pA[1]=(1,0);

for (int i=1; i<=n-1; i+=1)
  {
    pA[i+1]=pA[i]+unit(rotate(90)*(pA[i]-pO));
  }

for (int i=2; i<=n; i+=1)
  {
    draw(pO--pA[i-1]--pA[i]--cycle);
    markrightangle(pO,pA[i-1],pA[i],1.5mm);
    dot(format("$\mathrm{P}_{%i}$",i), pA[i],dir(pO--pA[i]));
  }

dot("$\mathrm{P}_{1}$", pA[1], dir(pO--pA[1]));