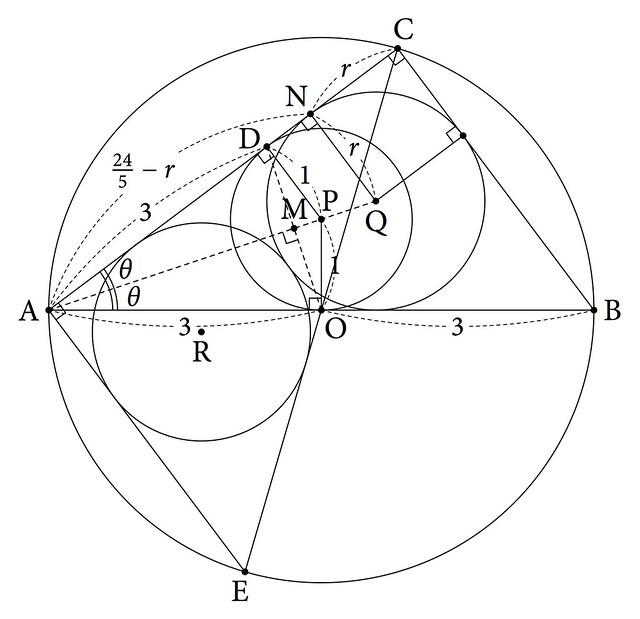
twitterのTLで今年のセンター試験・数学IAが難しくなってる,傾向が今までと違う,等々あったので,検索して問題をDLしてみた。いままでのセンターの問題とかほとんど見たことないので,どこがどう違うのかは分からないものの,第3問の幾何がちょっと面白そうだったので,図を描いてみた。
図が描いてあれば易しい問題だと思う。文章をちゃんと読んで,正しい図を描くことが存外難しいということなのであろう。
$\angle PAO=\theta$ とおけば,$\tan\theta=\frac{1}{3}$であるから,$\tan 2\theta=\frac{3}{4}$ となる。よって,三角形ABCは3辺の長さの比が$3:4:5$の直角三角形である。$AB=6$であるから,$AC=\frac{24}{5}$ となる。
三角形ABCの内接円の半径$r$は,この場合は直角三角形であるから,次のように相似を利用して簡単に求められる。
\[ AN:NC=AN:NQ=AD:DP=3:1 \]
であるから,
\[ r=\frac{1}{4}AC=\frac{6}{5} \]
これから,三角形ADPと三角形ANQの相似比は$5:6$と分かるから,
\[ PQ=\frac{1}{5}AP=\frac{\sqrt{10}}{5} \]
なお,図版は asymptote で描いた。備忘録的にソースを書いておく。
import fontsize;
defaultpen(fontsize(11));
dotfactor=6;
//pen dashed=linetype("6 6");
// pen dashed=linetype("3 3");
pen dashed=linetype("4 4");
pen thick=linewidth(0.6bp); // 太線用のペンを定義する。
pen hairline=linewidth(0.3pt);
defaultpen(linewidth(0.4bp)); // 線の太さを0.4ポイントに設定
// usepackage("amsmath");
usepackage("MinionPro");
import geometry;
/* 2点A, Bを結ぶ弧 */
path ConnectTwo(pair A, pair B, real OffSet) {
pair M=(A+B)/2+OffSet*unit(B-A)*I;
return A..M..B;
}
size(8cm,0);
point pO=(0,0), pP=(0,1);
circle cO=circle(pO,3), cP=circle(pP,1);
line T1=tangent(cP,pO-pP);
point[] pAB=intersectionpoints(T1,cO);
point pA=pAB[0], pB=pAB[1];
line tgs[]=tangents(cP,pA);
line T2=tgs[1];
point pD=intersectionpoints(T2,cP)[0];
point pC=intersectionpoints(T2,cO)[1];
point pE=2*pO-pC;
circle icABC=incircle(pA,pB,pC);
circle icCEA=incircle(pC,pE,pA);
point pQ=icABC.C, pR=icCEA.C;
point pT1=intersectionpoints(icABC,pA--pC)[0];
point pT2=intersectionpoints(icABC,pB--pC)[0];
point pM=intersectionpoints(pA--pP,pO--pD)[0];
real dist=0.15;
draw(Label(scale(0.9)*"\kern -0.5em\raise 1ex\hbox{$\frac{24}{5}-r$}", align=Center,filltype=UnFill), ConnectTwo(pA,pT1,3.7dist), hairline+dashed);
draw(Label(scale(0.9)*"$3$", align=Center,filltype=UnFill), ConnectTwo(pA,pD,1.5dist), hairline+dashed);
draw(Label(scale(0.9)*"$3$", align=Center,filltype=UnFill), ConnectTwo(pA,pO,-1.2dist), hairline+dashed);
draw(Label(scale(0.9)*"$3$", align=Center,filltype=UnFill), ConnectTwo(pO,pB,-1.2dist), hairline+dashed);
draw(Label(scale(0.9)*"$1$", align=Center,filltype=UnFill), ConnectTwo(pD,pP,dist), hairline+dashed);
draw(Label(scale(0.9)*"$1$", align=Center,filltype=UnFill), ConnectTwo(pO,pP,-dist), hairline+dashed);
draw(Label(scale(0.9)*"$r$", align=Center,filltype=UnFill), ConnectTwo(pT1,pQ,dist), hairline+dashed);
draw(Label(scale(0.9)*"$r$", align=Center,filltype=UnFill), ConnectTwo(pT1,pC,dist), hairline+dashed);
draw(cO);
draw(cP);
dot("A",pA, dir(pO--pA));
dot("B",pB,dir(pO--pB));
dot("O",pO,dir(pD--pP));
dot("D",pD,0.7dir(pQ--pD));
dot("C",pC,dir(pO--pC));
dot("P",pP,dir(pO--pQ));
dot("E",pE,dir(pO--pE));
dot("Q",pQ,dir(pP--pO));
dot("R",pR,dir(pP--pO));
dot("N",pT1,dir(pQ--pT1));
dot(pT2);
draw(pP--pO);
draw(pP--pD);
draw(pA--pB);
draw(pA--pC--pB);
draw(pC--pE--pA);
draw(icABC);
draw(icCEA);
draw(pQ--pT1);
draw(pQ--pT2);
draw(pO--pD,dashed);
draw(pA--pQ,dashed);
dot("M",pM,N);
markrightangle(pP,pO,pA,1.5mm);
markrightangle(pA,pD,pP,1.5mm);
markrightangle(pA,pC,pB,1.5mm);
markrightangle(pE,pA,pC,1.5mm);
markrightangle(pA,pM,pO,1.5mm);
markrightangle(pA,pT1,pQ,1.5mm);
markrightangle(pC,pT2,pQ,1.5mm);
markangle(scale(0.9)*Label("$\theta$"),radius=8mm,n=2,space=0.6mm, pO,pA,pP);
markangle(scale(0.9)*Label("$\theta$"),radius=8mm,n=2,space=0.6mm, pP,pA,pC);
addMargins(2mm,2mm);