[Σ]Sukarabe's Easy Living: 数学アーカイブ

2007年10月23日（火曜日）

NHKスペシャル「ポアンカレ予想」 [ 数学 ]

昨日、NHKでポアンカレ予想についての番組をやっていた。録画しておいて今日ゆっくり見たのだが、やっぱりテレビで数学の解説は難しいのかなあ、という感想。

まあ、ポアンカレ予想というトポロジー(位相幾何学)の難問があり、サーストンの幾何化予想を経て、ペレリマンによって最終的に解決されたことは分かった。しかし、ポアンカレ予想の説明はどうだったろうか。あれでは宇宙の形を決定する問題だと誤解されてもしかたがないように思う。宇宙を引き合いに出したのは単なる例であるのに、まるでそれが問題であるかのようなナレーション。基本群とかホモトピーとかいう用語は出す必要ないと思うけど、宇宙とかではなく、もう少しきちんと説明した方が良かったのではないかしら。３次元の閉じた図形(境界のない多様体)があり、それに含まれるどんな閉曲線も一点に縮めることができるならば、その図形は３次元球面に同相である(１対１連続に変形できる)、とか。やっぱり無理があるか？

投稿者 sukarabe : 21:26 | この記事の固定URI | コメント (4) | トラックバック (1)

2007年09月01日（土曜日）

ガロア群が巡回群となる３次方程式について (５) [ 数学 ]

こんなに長くなるのでは書くのではなかったか・・・と後悔しつつも(苦笑)、今回でやっと終わり。

今までの結果をまとめると次のようになる。多項式 $f(x)=x^3-x+\frac{1}{3}$ に対して、方程式 $f(x)=0$ の任意の解 $\alpha$ をとる。このとき、これ以外の2解を $\beta$ , $\gamma$ とすると、差積
$\Delta=(\alpha-\beta)(\alpha-\gamma)(\beta-\gamma)$
に対して、
$\Delta^2=1, \qquad \Delta=\pm1$
が成立する。必要ならば $\beta$ , $\gamma$ を入れ替えて $\Delta=1$ としてよく、
$\beta-\gamma=\frac{\Delta}{(\alpha-\beta)(\alpha-\gamma)}=\frac{\alpha}{2\alpha-1}=6\alpha^2+3\alpha-4$
$\beta+\gamma=-\alpha$ であったから、
$\beta=3\alpha^2+\alpha-2, \qquad \gamma=-3\alpha^2-2\alpha+2$
となる。これから、 $\varphi(x)=3x^2+x-2$ とおけば、
$\beta=\varphi(\alpha), \quad \gamma=\varphi(\beta), \quad \alpha=\varphi(\gamma)$
も分かる。

というわけで、この項目はこれで終わりです。

投稿者 sukarabe : 08:46 | この記事の固定URI | コメント (3) | トラックバック (0)

2007年08月31日（金曜日）

ガロア群が巡回群となる3次方程式について (4) [ 数学 ]

最後の作業は $2\alpha-1$ の逆数を $\alpha$ の多項式として表すこと。 $\alpha$ は方程式
$f(x)=x^3-x+\frac{1}{3}=0$
の根であるから、これは商体 $\mathbb{Q}[x]/(f)$ における $2x-1$ の逆元を求めることと同じ。さらに言い換えると、多項式環 $\mathbb{Q}[x]$ において、合同式 $(2x-1)P(x)\equiv 1\ ({\rm mod}\, f)$ を満たす多項式 $P(x)$ を求めることと同じ。さらにさらに言い換えると、多項式環 $\mathbb{Q}[x]$ において
$(2x-1)P(x)-f(x)Q(x)=1$
を満たす $P(x)$ , $Q(x)$ を(どれか一つで良いから)求めることと同じ。ちょっとくどくなったが、これで(多項式環における)不定方程式の話になった。

これを解くには整数の不定方程式の場合と同じく、ユークリッドのアルゴリズム(いわゆる互除法)を用いればよい。この場合は $2x-1$ が1次式であるから、 $f(x)$ を $2x-1$ で1回割ればよい。結果は次の通り。
$f(x)=\frac{1}{8}(2x-1)(4x^2+2x-3)-\frac{1}{24}$
これに $x=\alpha$ を代入すれば、 $f(\alpha)=0$ であるから、
$\frac{1}{2\alpha-1}=12\alpha^2+6\alpha-9$
以上で $2\alpha-1$ の逆数を $\alpha$ の多項式で表すことができた。これから、
$\frac{\alpha}{2\alpha-1}=12\alpha^3+6\alpha^2-9\alpha=12\left(\alpha-\frac{1}{3}\right)+6\alpha^2-9\alpha=6\alpha^2+3\alpha-4$
となる。

投稿者 sukarabe : 21:34 | この記事の固定URI | コメント (0) | トラックバック (0)

ガロア群が巡回群となる3次方程式について (3) [ 数学 ]

前回は $\Delta^2=1$ を求めるところまでだった。これから $\Delta=\pm 1$ となる。符号は根の順番で変わるから、必要なら $\beta$ と $\gamma$ を入れ替えて $\Delta=1$ としてよい。このとき、
$\beta-\gamma=\frac{1}{(\alpha-\beta)(\alpha-\gamma)}$
となる。分母は、
$(\alpha-\beta)(\alpha-\gamma)=\alpha^2-(\beta+\gamma)\alpha+\beta\gamma=2\alpha^2-\frac{1}{3\alpha}=\frac{6\alpha^3-1}{3\alpha}$
であるが、 $\alpha^3=\alpha-\frac{1}{3}$ であるから、
$(\alpha-\beta)(\alpha-\gamma)=\frac{6\alpha-2-1}{3\alpha}=\frac{2\alpha-1}{\alpha}$
これを上の $\beta-\gamma$ の式に代入すれば、
$\beta-\gamma=\frac{\alpha}{2\alpha-1}$
となる。これを $\alpha$ の多項式で表すところまでやるつもりだったが、今回はここで終了する。以下は次回にもちこし。

投稿者 sukarabe : 13:26 | この記事の固定URI | コメント (1) | トラックバック (0)

2007年08月30日（木曜日）

ガロア群が巡回群となる3次方程式について (2) [ 数学 ]

具体例として、コメント欄で出題されていた方程式 $f(x)=x^3-x+\frac{1}{3}=0$ を考えてみる。あまり省略せずに書くために、数回に分けることにする。最初は差積 $\Delta$ の2乗、つまり判別式の値を計算する。
$\Delta^2=(\alpha-\beta)^2(\alpha-\gamma)^2(\beta-\gamma)^2$
である。最初の因数は
$(\alpha-\beta)^2=(\alpha+\beta)^2-4\alpha\beta=(-\gamma)^2-4\cdot\frac{-1}{3\gamma}=\frac{3\gamma^3+4}{3\gamma}$
となる。 $\gamma$ は $f(x)=0$ の解であるから、 $\gamma^3=\gamma-\frac{1}{3}$ となるので、代入すると
$(\alpha-\beta)^2=\frac{3\gamma-1+4}{3\gamma}=\frac{\gamma+1}{\gamma}$
他の因数も同様であるから、
$\Delta^2=\frac{(\alpha+1)(\beta+1)(\gamma+1)}{\alpha\beta\gamma}$
となる。 $\alpha\beta\gamma=-\frac{1}{3}$ であり、また $(\alpha+1)(\beta+1)(\gamma+1)$ は、展開して解と係数の関係を用いると、
$(\alpha+1)(\beta+1)(\gamma+1)=-\frac{1}{3}-1+0+1=-\frac{1}{3}$
となる。従って、 $\Delta^2=1$ である。

今回はここまで。次回は、 $\alpha$ の有理式を2次式で表す話が中心となる予定。

投稿者 sukarabe : 19:42 | この記事の固定URI | コメント (1) | トラックバック (0)

ガロア群が巡回群となる3次方程式について (1) [ 数学 ]

まあ、せっかくコメントして頂いた(苦笑)ことだし、ちょっとだけ。というか、さしせまった原稿があるワタシとしては、こんなことしている場合ではないのだが。逃避行動なのか？(爆)

一般の3次方程式は $x^3+ax^2+bx+c=0$ という形であるが、 $x+\frac{a}{3}=t$ とおけば $t^3+pt+q=0$ の形に変形される。よって $x^3+px+q=0$ で考えても一般性を失わない。この3次方程式のガロア群は一般的には3次対称群 $S_3$ であるが、特別な場合、具体的には判別式 $D$ の平方根が基礎体(ここでは有理数体 $\mathbb{Q}$ とする)に属するときには3次交代群 $A_3$ になる。この場合には、3つの解(根) $\alpha$ , $\beta$ , $\gamma$ に対して、
$\varphi(\alpha)=\beta, \quad \varphi(\beta)=\gamma, \quad \varphi(\gamma)=\alpha$
となる有理数係数の多項式 $\varphi(x)$ を具体的に求めることができる。

判別式 $D$ は差積 $\Delta=(\alpha-\beta)(\alpha-\gamma)(\beta-\gamma)$ の2乗であるから、上の条件は差積 $\Delta$ が基礎体 $\mathbb{Q}$ に属することと同じである。解(根)と係数の関係から
$\beta+\gamma=-\alpha, \quad \beta\gamma=-\frac{q}{\alpha}$
であることに注意すれば、
$\beta-\gamma=\frac{\Delta}{(\alpha-\beta)(\alpha-\gamma)}=\frac{\Delta}{2\alpha^2-\frac{q}{\alpha}}$
となり、これは $\alpha$ の多項式で表すことができる。 $\beta+\gamma$ も $\alpha$ の多項式で表されているから、これで問題は解けたことになる。

次回はコメントにあった具体的な方程式 $x^3-x+\frac{1}{3}=0$ に対して、 $\varphi(x)$ を求める予定。

投稿者 sukarabe : 09:07 | この記事の固定URI | コメント (3) | トラックバック (0)

2007年08月21日（火曜日）

シグマの公式と組合せの話 [ 数学 ]

先日、知り合いに教わった $\sum_{k=1}^{n}k^2$ の求め方。知ってる？って聞かれて、いや、と答えたのだが、なんかDeja-vuのような気もする。最近、すぐに忘れるから(笑)。以下で組合せの記号が出てくるが、普通 ${}_n{\rm C}_r$ と書くところを、ここでは $C(n,r)$ と書く。mimeTeXでこれを書くと、ときどきうまく行かないものだから。

$n$ を自然数として、 $1\leq x<z\leq n+1$ , $1\leq y<z\leq n+1$ を満たす整数の組 $(x,y,z)$ の個数を考えるのだという。なるほど。 $z=k+1$ と固定すれば、 $x$ , $y$ はそれぞれ $1$ から $k$ の $k$ 通りずつだから、 $(x,y)$ のペアは $k^2$ 通り。それを $k=1$ , $2$ , $\cdots$ , $n$ でシグマすれば良いから、 $\sum_{k=1}^{n}k^2$ になる。

これを別の方法で数えようというのであった。 $x$ と $y$ が等しいか否かで場合分けする。 $x=y$ のときは、 $1$ から $n+1$ から異なる2個を選んで、大きい数を $z$ , 小さい数を $x$ と $y$ にすればよいので、 $C(n+1,2)$ 通り。 $x\neq y$ のときは、 $1$ から $n+1$ から異なる3個を選ぶことになる。最大のものを $z$ とし、残りを $x$ と $y$ に割り振る。どちらを $x$ にするかで2倍だけあるから、 $C(n+1,3)$ の2倍。以上を合わせれば、上の $\sum_{k=1}^{n}k^2$ に一致するはずだから、
$\sum_{k=1}^{n}k^2=C(n+1,2)+C(n+1,3)\times2=\frac{n(n+1)}{2}+\frac{n(n+1)(n-1)}{6}\times2$
となる。

ふーん、いろんな事を考えるものだ。それにしても、やっぱり、何処かで読んだことあるかも・・・。

投稿者 sukarabe : 14:23 | この記事の固定URI | コメント (4) | トラックバック (0)

2007年07月23日（月曜日）

ポンスレーの閉形定理、文献メモ [ 数学 ]

数学セミナーのバックナンバーにポンスレーの閉形定理の記事があることを知った。筆者はOort(オールト)およびBos(ボス)で、上野健爾さんの訳。1986年の5月号から8月号にかけて連載されている。参考文献として、Bos, Kers, Oort, Raven共著になる近刊のプレプリントが載っているが、それって次と同じものだろうか？
H J M Bos, C Kers, F Oort and D W Raven, Poncelet's closure theorem, Exposition. Math. 5 (4) (1987), 289-364.
というか、この論説と上野先生が翻訳されたものの関係はどうなっているのかな？いずれにせよ、日本語でかなり詳しい説明が読めるのはありがたい。

投稿者 sukarabe : 23:33 | この記事の固定URI | コメント (0) | トラックバック (0)

2007年05月06日（日曜日）

レムニスケートの有理パラメータ表示 [ 数学 ]

以前、Sa氏からレムニスケートって有理曲線なんだよね、と教わったことがある。へえ～と思ったのだが、パラメータ表示のやり方がこれまたへえ～なのだった。どうするのかと言うと、レムニスケート $(x^2+y^2)^2=a^2 (x^2-y^2)$ に対して、原点で接する円束(Pencil of Circles) $x^2+y^2=t(x-y)$ との交点を考えれば、 $t$ でパラメトライズできるというのだ。シャファレビッチの代数幾何の教科書に書いてあるよ、ということだったので、調べてみたところ、確かに Basic Algebraic Geometry の演習問題に載っていた。直線束でパラメトライズするのは常套手段なのだが、円束とは！と驚いた記憶がある。

その後、レムニスケートが双曲線の反転で得られるという、これまた意外な結果を誰かから教わったりしたのだが、そのときはこの二つの事実の関連性に気付かなかった。

先日、シャワーを浴びながらの髭剃り中にぼんやり考えていたら、あ！と気がついた。双曲線は無限遠点を通る直線束、つまり漸近線に平行な直線束によりパラメータ表示されるが、これを反転すれば、レムニスケートと円束になるではないか、と。反転は双有理変換であるから、有理性も保たれる。そうか、そうだったのか。ちょっと嬉しいのである(^_^)。

投稿者 sukarabe : 12:55 | この記事の固定URI | コメント (3) | トラックバック (0)

2007年05月05日（土曜日）

インドの数学教育 [ 数学, 雑記 ]

テレビでインドの数学教育についてやっている。覚えるのではなく、考え方に重点を置いているそうだ。あたりまえだと思うが、最近の日本では違うらしい。答えがあっていてもプロセスが間違っていると正解にならないらしい。そんなの当たり前でしょ？あ、そうか、日本では○×式だから分からないか(笑)。考え方をとことん説明する証明が重視されているらしい。ワタシが中学生の頃は、まだ証明問題とかあったんだがなあ、日本でも。

要するに、あたりまえの普通の教育ってことでしょ？それが行われていないらしい今の日本が不思議。

へえ～っと思ったのが2桁の掛け算でのTIPS。たとえば、６５×６５のように一の位が５のときは、次のようにするのだそうだ。下二桁は五五二十五で２５になる。上の二桁は、六七四十二として４２。結果として、４２２５が答え。ふーん、確認してみよう。これって２乗の場合ってことで良いのかな？二桁の自然数 $N$ を、 $N=10a+5$ とおく。 $a$ は一桁の数。すると、
$N^2=(10a+5)^2=100a^2+100a+25=100a(a+1)+25$
となる。なるほど、確かに正しい。しかし、こんなことまで覚えるのは(たとえ理由を分かっていても)ちょっと違和感あるな。こんなことで数秒早くできても意味はあまりないと思う。

投稿者 sukarabe : 08:36 | この記事の固定URI | コメント (0) | トラックバック (0)

2007年03月14日（水曜日）

気付いてしまえば簡単なのだが [ 数学 ]

散々苦労したので、腹立ちまぎれに。もっとも自分の頭が悪くなっているのに腹を立てるべきなのかもだが(苦笑)。

何の因果か、小難しそうな問題を解く羽目に。式の意味というか手続きの意味を考えれば直観的には明らかに思えるのだが、有限回の操作で定常状態になることがなかなか証明できない。とすれば途中に現れる数列
$J_n=\sum_{i=1}^{m} (x_i-p_n)^2+\sum_{j=m+1}^{N} (x_j-q_n)^2$
が広義の減少列であることを利用するのだろうか。しかしなあ、極限を考えたところで、十分大きな $n$ に対して $J_n$ が一定になることは言えそうもない。ううむ、困った。あれこれ考えること数十分。ふと、 $J_n$ に現れる変数たちが連続変数でないことに気付く。というか、与えられた有限数列 $\lbrace x_i\rbrace\ (1\leq i\leq N)$ の一部分の平均となる $p_n$ , $q_n$ は有限通りの値しかとれない。 $m$ も同じ。ということはどんなに頑張ってみても、 $J_n$ の取り得る値というのは有限個しかないではないか！ああ、何ということだ。意識下でこんなことはずっと考えていたように思う。この手のトリックは手馴れたものであるからして、昔だったら直ちに気付いていたはずだ。薄々気付いていたことが意識に上らなくなることが最近多い。これも歳かなあ・・・orz...

ということで、 $J_n$ の取り得る値は有限通りなので、広義単調減少ということと合わせれば、無限個の $n$ で $J_n>J_{n+1}$ ということはありえない。つまり、ある番号から先ではつねに $J_n=J_{n+1}$ となるはずである。ふう～、これで多分一件落着だと思う。何か勘違いしてなければ・・・。

投稿者 sukarabe : 02:29 | この記事の固定URI | コメント (6) | トラックバック (0)

2007年02月05日（月曜日）

単位円の群構造 [ 数学 ]

知っている内容でも、別の表現や立場から見直してみると面白いことがある。

単位円 $x^2+y^2=1$ は点 $(1,0)$ を単位元とするアーベル群になる。群の演算を＋で表すと、
$(a,b)+(c,d)=(ac-bd,ad+bc)$
となる。これは複素数の掛け算とも考えられるし、また、三角関数の加法定理と考えることもできる。それはともかく、有理点に対してこれを行うと、ピタゴラス数と関係する。

$3^2+4^2=5^2$ , $5^2+12^2=13^2$ であるから、 $P=$\frac{3}{5},\frac{4}{5}$$ , $Q=$\frac{5}{13},\frac{12}{13}$$ は単位円上の有理点。この２点の和を作ると、
$P+Q=$\frac{3}{5}\cdot\frac{5}{13}-\frac{4}{5}\cdot\frac{12}{13}, \ \frac{3}{5}\cdot\frac{12}{13}+\frac{4}{5}\cdot\frac{5}{13} $=$-\frac{33}{65},\ \frac{56}{65}$$
もまた単位円上の有理点。つまり、 $33^2+56^2=65^2$ となり、新たなピタゴラス数が得られたことになる。

まあ、結局はブラフマグプタの恒等式
$(a^2+b^2)(c^2+d^2)=(ac-bd)^2+(ad+bc)^2$
に他ならないというか、この恒等式が正に群構造を与えているということなんだが。

投稿者 sukarabe : 12:22 | この記事の固定URI | コメント (0) | トラックバック (0)

テータ関数とは [ 数学 ]

[メモ] 楕円関数はトーラス $\mathbb{C}/L$ 上の有理型関数だが、テータ関数はトーラス上の関数にはならない。では、何なのか？ $\mathbb{C}/L$ 上のライン・バンドルのセクションと考えれば良いんだね。そうか、なるほど！

投稿者 sukarabe : 00:33 | この記事の固定URI | コメント (0) | トラックバック (0)

2007年02月03日（土曜日）

楕円関数の勉強予定 [ 数学 ]

いろんな本をひっくり返し眺めてみると、なかなか難しいなあと思う。楕円積分の逆関数という路線で始めようとすると、逆関数が一価であることすら証明が容易ではない、とかね。

いつまでも悩んではいられないので、安藤四郎著「楕円積分・楕円関数入門」をテキストとして勉強することに決定。ただ、テータ関数の導入がちょっとだけ気に入らないので、そこはKoenigsbergerか何かで補って、snの無限積展開に関連させることにしよう。それから、上記の逆関数の一価性の部分は、Siegelに証明があったと思うので、それで補う、と。一応、こんなところで良いかな？

投稿者 sukarabe : 00:06 | この記事の固定URI | コメント (1) | トラックバック (0)

2007年01月31日（水曜日）

クヌースの本にもcontinuantあった [ 数学 ]

Continuantの計算とかやっていると、非常にアルゴリズム的な色彩が強い。してみると案外クヌース(Knuth)先生の本とかに書いてあるかもと調べてみた。すると、Concrete Mathematics の278ページにその名もずばり、Continuants という節があった。そこでは、
$\begin{align} K_0()&=1\\ K_1(x_1)&=x_1 \\ K_{n}(x_1,\cdots,x_n)&=K_{n-1}(x_1,\cdots,x_{n-1})x_n+K_{n-2}(x_1,\cdots,x_{n-2}) \end{align}$
により定義してあった。変数の個数に応じてcontinuantの方も添え字で区別する方が、確かに理にかなっているかな。もっとも、変数の個数が分かっているときは、単に $K$ と添え字を省略するとも書かれていたが。

ずっと読んでいくと、オイラー (Euler) が次のような法則性を発見していた、と書いてあった。例えば、変数が4個のときは、
$K(a,b,c,d)=abcd+ab+ad+cd+1$
となるのであるが、これは次のようにして得られると。まず、変数全部をこの順番に並べたもの、abcdを作る。次に、隣り合った二つの積を消していくという操作を可能なすべてのパターンに渡って行う。今の場合は、
abcd, abcd, abcd, ab cd
つまり、 $cd$ , $ad$ , $ab$ , $1$ となる。以上をすべて足し合わせればよい。これは、モールス信号のパターンと対応している。

残念ながら、このことの証明は書かれていなかった。ちょっと残念。これを認めるならば、組合せ的な考え方で、いろんな等式の証明ができるみたいなのだが。

投稿者 sukarabe : 13:25 | この記事の固定URI | コメント (0) | トラックバック (0)

ささやかな幸せ [ 数学 ]

例のcontinuantの等式を行列を用いてすっきりと証明できた。まあ、探せば既に知られている事だとは思うが、久しぶりに自分で考えたので、ちょっと嬉しい。

continuantというのは、 $n$ 個の不定元(変数)からなる多項式 $K(a_1,\ldots,a_n)$ で、連分数を普通の分数で表したときに現れるもの。例えば、
$a+\frac{1}{b+\frac{1}{c+\frac{1}{d}}}=\frac{K(a,b,c,d)}{K(b,c,d)}$
となる。ポイントは次のタイプの等式
$\begin{array}K(a,b,c,d,e)&K(a,b,c,d)\\ K(b,c,d,e)&K(b,c,d)\end{array}\) = $\begin{array}a&1\\ 1&0\end{array}$ $\begin{array}b&1\\ 1&0\end{array}$ $\begin{array}c&1\\ 1&0\end{array}$ $\begin{array}d&1\\ 1&0\end{array}$ \(\begin{array}e&1\\ 1&0\end{array}$

これから、まず、転置行列を取る事により、
$K(a,b,c,d,e)=K(e,d,c,b,a)$
といった「反転公式」を証明できる。また、行列の積を二つに分割することで、
$K(a,b,c,c,b,a)=K(a,b,c)^2+K(b,c)^2$
のタイプの等式が導かれる。これらが、Henry J. S. Smithによるフェルマーの定理の証明の基礎となる。

投稿者 sukarabe : 00:19 | この記事の固定URI | コメント (0) | トラックバック (0)

2007年01月30日（火曜日）

連分数とフェルマーの定理(追記) [ 数学 ]

最近の論文で、Henry J. S. Smithによるフェルマーの定理(4で割って1余る素数は、2個の平方数の和として表せる) の証明、および、表現の一意性について書かれているものを見つけた。PDFが文字化け(というか多分フォントの埋め込み関係かな)で読めないのだが、幸いTeXファイルも一緒に置いてあるので、次のディレクトリーからTeXファイルを落としてきて、自分でコンパイルすると読める。
http://www.emis.de/journals/INTEGERS/papers/f30/

continuant $K(a_0,a_1,\cdots,a_n)$ についての等式が組合せ的な解釈で証明できるというのは新鮮で面白い。

投稿者 sukarabe : 14:03 | この記事の固定URI | コメント (0) | トラックバック (0)

2007年01月29日（月曜日）

クリスタルの代数学教科書 [ 数学 ]

クリスタル(Chrystal)の代数学(Algebra)の教科書は、明倫館で手に取って眺めたことはあるが、なにせ19世紀末の古い本で、しかも所謂学校で教える代数(群論とかガロア理論とか以前の初等代数)の教科書であるため、特別興味もなかった。今回、Henry J. S. Smithによる $p=x^2+y^2$ の証明をきっかけに少し読んでみた。大部な本なので、もちろん全部を読んだわけではないが、高校の数学と大学の数学の中間ぐらいのレベルで、しかも今のカリキュラムでは教わらない面白い事柄がいくつかあるようで、へえ～と思った。今度神保町に寄ったとき、安かったら(←ここ重要、笑)買ってみようかな。まあ、PDFあるからそれでもいいが。

とりあえず、第2巻の第34章「一般の連分数」をプリントアウトした。連分数のcontinuantに関する性質は、高木貞治の「初等整数論入門」や藤原松三郎の「代数学」にも一部はあるが、クリスタルの方が詳しい。ここに書かれている内容は初等的で難しくはないが、単純な式変形なので見通しが良くない。行列を使って、もう少し見通しの良い証明とかできないかなあと、思案中なのだが。

[追記] 序文が次のページで読める。 Preface to Chrystal's "Algebra"

投稿者 sukarabe : 14:57 | この記事の固定URI | コメント (0) | トラックバック (0)

2007年01月28日（日曜日）

連分数とフェルマーの定理 [ 数学 ]

ここでいうフェルマーの定理というのは、4で割って1余る素数は2個の平方数の和で書ける、というもの。比較的初等的な証明をHenry J. S. Smithが与えていると、どこかに書いてあったので調べてみることに。

H. J. S. Smithの全集第1巻がInternet Archiveにあるので、1855年の論文を読もうとしたのだが、ラテン語のため挫折。2ページの短いやつなので山勘で読めなくもないのだが、ロジックの肝心な部分がやはり駄目だった。素数 $p$ に対して、 $\frac{p}{m}$ の連分数展開を考えるというもの。一体どうするのやら。

いろいろ調べてみると、クリスタルの代数学の教科書(2巻本)に証明が載っているらしいので、ChrystalのAlgebraを探すのだが、Internet Archiveにも、MichiganにもCornellにもない。専門書じゃなく、(19世紀末ごろの)高校の教科書みたいなものだからかなあ。ともあれ、http://onlinebooks.library.upenn.edu/webbin/book/lookupid?key=olbp36404 なる謎の(？)ページに辿り着き、何とかPDFをダウンロード。ここもアーカイブか何かだろうか？

クリスタルの第2巻に、確かにSmithによる証明というのが載っていた。具体例もついていて理解できる。なるほど！ $p=4n+1$ の素数に対して、分母 $m$ が $\frac{p}{2}$ より小さい、つまり $2n$ 以下のものをすべてとり、2より大の既約分数 $\frac{p}{m}$ を考える。これら $2n$ 個の既約分数を連分数展開すると、 $p$ は $2n$ 通りのcontinuantとして表される。continuantというのは、連分数を普通の分数に戻したときにできる式のこと。例えば、
$a+\frac{1}{b+\frac{1}{c}}=\frac{abc+a+c}{bc+1}$
なので、
$[a,b,c]=abc+a+c, \quad [b,c]=bc+1$
などと書き、これをcontinuantと呼ぶ。これに関しては幾つかのきれいな関係式がなりたつのだが、それらは初等数論(高木貞治の初等整数論講義など)の本にあるので、ここでは省略。

このcontinuantの性質として、変数を左右逆転させても値が同じというものがある。従って、 $p$ が
$p=[a,b,c,d]$
と表されたとすれば、
$p=[d,c,b,a]$
も成り立つ。この様な表現が全部で $2n$ 通り、つまり偶数個あるのだが、そのうち、 $p=\frac{p}{1}$ に対応する $p=[p]$ という左右対称なものが1つあるのだから、もう一つ左右対称な表現が存在するはずだ、というのがポイント。この左右対称なcontinuantから $p$ が2個の平方数の和に表されることが示される。 $p=[a,b,c,c,b,a]$ ならば、
$p=[a,b,c,c,b,a]=[a,b,c]^2+[a,b]^2$
というように。このあたり、continuantに関する少し詳しい知識が必要になってくる。

具体例を一つ。 $p=13$ の場合、 $m=5$ に対して
$\frac{13}{5}=2+\frac{1}{1+\frac{1}{1+\frac{1}{2}}}$
となるので、
$13=[2,1,1,2]=[2,1]^2+[2]^2=3^2+2^2$

うーん、確かに初等的ではあるが、連分数論の初歩を学んでいないと、ちょっとつらいかな？今のカリキュラムだと数学科でもあまりやらなそうな古典的分野ではあるな。しかし、非常に面白い内容で、満足。

投稿者 sukarabe : 15:35 | この記事の固定URI | コメント (0) | トラックバック (0)

2007年01月13日（土曜日）

奇妙な式変形 [ 数学 ]

[備忘録] 多分大分前に何処かで出会っている気がするが，ふと思い出したというか脳裏に蘇ったので記録。

$\int \frac{1}{\sin x}\,dx=\log\|\tan\frac{x}{2}\|$ の導き方。見やすくするために $x=2t$ と書く。すると，
$\begin{align} \int \frac{1}{\sin x}\,dx &=\int \frac{\cos^2t+\sin^2t}{\sin t\cos t}\,dt =\int$\frac{\cos t}{\sin t}+\frac{\sin t}{\cos t}$\,dt \\ &=\log\|\sin t\|-\log\|\cos t\|=\log\|\tan t\| \\ &=\log\|\tan\frac{x}{2}\| \end{align}$
となる。

投稿者 sukarabe : 09:30 | この記事の固定URI | コメント (0) | トラックバック (0)

2007年01月06日（土曜日）

船頭多くして・・・ [ 数学 ]

楕円関数をざっと復習して例の恒等式の証明まで進みたいのだが、天下りの定義が嫌いな性分が災いしてなかなか進まない。いろいろ読んだ結果、天下りではあるがテータ関数をまず定義して、それからスタートするのが最も効率的であり、論理的にもすっきりすることは理解できた。しかしなあ・・・その道は嫌いじゃ(笑)。少なくとも、テータ関数がどのように発生するのか、ある程度自然な議論が欲しい。うーむ。

ということで鋭意勉強中なのだが(笑)、一冊ではまかないきれず数冊の参考書を比較検討しながら進めているので、これがなかなかに面倒。ちなみに関数論を一切使わないで歴史的に進めようとしているわけではない。関数論は使うが、動機を大切にしたいということなのであった。あー面倒だ(苦笑)。それでは寸評。

安藤四郎「楕円積分・楕円関数入門」
入門書であり、非常に丁寧に書かれていて読みやすい。最初は実変数で議論しているが、複素変数になってからは、改めてリーマン面上での楕円積分を考え、その逆関数として sn(u) などを導入している。テータ関数は sn(u) の極を零点とする整関数を作ろう、という方針で導入されていて、これはこれで良いかとも思う。こうして書いていて思うのだが、この本の進め方って良いかも。これ一冊しか手元になければ迷いが無くて良かったかもだ(苦笑)。

Pierpont : Functions Of A Complex Variable
これは関数論全般の入門書であるが、後半に楕円関数の丁寧な入門がある。テータ関数の導入は、sn(u)の無限乗積展開から始めている。ただし、無限乗積のところは、アーベルはこんな風にして導いたと方針のみのお話。まあ、動機付けだからこれで良いのかな？

Koenigsberger : Vorlesungen über die Theorie der elliptischen Functionen, nebst einer Einleitung in die allgemeine Functionenlehre, Teubner (1874)
ドイツ語なので数式以外が分からない(苦笑)のだが、眺めてみたところ、なかなか良さそう。非常に長いのだが、305ページから327ページまでの20ページ余りを読めば、当面の目標は果たせそう。上のPierpontの本で省略されている sn の無限乗積展開を導いている。

河田敬義「ガウスの楕円関数論」(上智大学数学講究録 No. 24)
これは高木貞治の「近世数学史談」にあるガウスの楕円関数発見の話を丁寧にフォローしたもの。ちょっと独特ではあるが、関数論の一般論を使わずに初等的変形で2重の無限積を1重の無限積さらに無限級数に変換する議論は面白く参考になる。

Walker : Elliptic Functions: A Constructive Approach
これもちょっと変わった入門書。Weilの Elliptic Functions according to Eisenstein and Kronecker に示唆されて、アイゼンシュタイン流の無限級数による楕円関数の導入を実際に行ったもの。絶対収束しない無限級数を扱うのでちょっと注意が必要だが、関数論をあまり使わずに初等的に議論できる。テータ関数の章は、2重無限積から無限級数への変換の扱いで参考になる。

投稿者 sukarabe : 10:12 | この記事の固定URI | コメント (0) | トラックバック (0)

2007年01月04日（木曜日）

Pierpont氏の複素関数論教科書 [ 数学 ]

もう随分前になるが、神保町でえらく古い(1914年の発刊)複素関数論の教科書を買った。いまさら入門書を買うこともないと思いつつも、楕円関数についてかなり丁寧に書かれていたので、ちょっと気に入ったのであった。今回、楕円テータ関数の復習というか再履修(笑)というかをするに当たって、本棚から引っ張り出してきた。

著者は James Pierpont という人。さして有名人でもないと思うが、念のため検索してみると、この教科書以外にはネットでは引っかからない。ふーむ。しかし、この本自体が Dover Phoenix Editionとして復刻されていることを発見。さらにミシガン大学のHistorical Math Collectionにもあった。

それにしても、日本の関数論の入門書は判で押したように、コーシーの積分定理、留数定理あたりで終わってしまう。そんな教科書が無数(？)にある。そこから先が面白いのに～。楕円関数を解説してあるものはほとんどなく、あったとしてもワイエルシュトラスの $\wp$ (ペー)関数をちょっとだけ。まあ、ページ数とかいろいろ理由はあるのだろうが。それに比べると外国の教科書、特に20世紀初頭の古い本は詳しくて楽しい。

Pierpont氏の教科書で気に入っていることの一つが天下りが少ないこと。例えばWhittaker-Watsonあたりだと、ヤコビの楕円関数をテータ関数の商として定義してある(笑)。まあね、結局は同じになるんだけどさあ、それはちょっとないんじゃないの？と言いたくなる。その点、Pierpont氏は良い。ヤコビの楕円関数を第1種楕円積分の逆関数として定義(ここをちゃんとやるにはリーマン面とかいろいろ面倒ではあるのだが・・・)したあと、アーベルによる無限積展開を示し、この導き方は厳密ではないのだが・・・しかし、これに示唆されて、次のような関数を考える・・・と、テータ関数を導入している。このようなゆったりした講義調の教科書を書くのは案外と大変であるから、多くの著者が簡潔で厳密で天下りの書き方に走ってしまうのは、何となく分かる。分かるんだけどね。

投稿者 sukarabe : 13:10 | この記事の固定URI | コメント (0) | トラックバック (0)

2007年01月03日（水曜日）

ヤコビのファンダメンタ・ノヴァ [ 数学 ]

Watsonの論文で「良く知られた等式」として
$q^{\frac12} \prod_{n=1}^{\infty} (1-q^{2n})^{6} = 2\pi^{-3}kk'K^3$
というものが使われており、JacobiのFundamenta Nova (楕円関数新論)が引用されている。当時の教育課程では常識だったのだろうか。他の楕円関数の教科書で探せるかもだが、一応御本尊を見ておくか。Gallica-Math: Œuvres complètes にヤコビの全集があり、PDFで読めるようになっている。第1巻の Carl Gustav Jacob Jacobi - Œuvres complètes, tome 1 から Fundamenta nova theoriae functionum ellipticarum を選んでダウンロード。あ、ラテン語だ、orz...

[追記] Internet Archive にもヤコビ全集の第1巻があった。 Internet Archive: Details: Gesammelte werke こっちの方がスキャンがきれいかも知れない。

投稿者 sukarabe : 13:00 | この記事の固定URI | コメント (0) | トラックバック (0)

一歩前進 [ 数学 ]

[備忘録] 例のラマヌジャンの連分数に関する G. N. Watson の論文。以前読んだときに挫折した箇所を久しぶりに再チャレンジ。こっちが近視眼的になっていたせいもあると思うが、もう少し丁寧に書いてくれよ～(苦笑)、という気持ち。とりあえず、今回はクリアーしました！

忘れないようにメモ。 $\prod_{n=1}^{\infty}(1-q^{n/5})$ を無限級数展開すると、オイラーの五角数定理によって、
$\prod_{n=1}^{\infty}(1-q^{n/5})=\sum_{n=-\infty}^{\infty}(-1)^{n}q^{n(3n+1)/10}$
となる。右辺の分数冪のうち、 $n\equiv 4 \pmod{5}$ に対応するものを考える。 $n=-5m-1$ と置けば、それに関する和は
$\sum (-1)^{m+1}q^{1/5+5m(3m+1)/2}$
となる。従って、これを $\prod_{n=1}^{\infty}(1-q^{5n})=\sum (-1)^{m}q^{5m(3m+1)/2}$ で割れば、商は $-q^{1/5}$ となる。以上から、 $J_1$ , $J_2$ を $q$ の整数冪の級数として、
$\prod_{n=1}^{\infty}\frac{1-q^{n/5}}{1-q^{5n}}=J_1-q^{1/5}+q^{2/5}J_2$
の形で表される。

あースッキリした～。奥歯に挟まっていた野沢菜がやっと取れた気分(笑)。分かってしまえば、なんだ、簡単じゃないか～。しかしねえ、盲点に入ると、これが分からないのよ～。

投稿者 sukarabe : 10:54 | この記事の固定URI | コメント (0) | トラックバック (0)

2006年12月29日（金曜日）

クラインの「高い立場からみた初等数学」 [ 数学 ]

クライン(Felix Klein)の「高い立場からみた初等数学」の英訳版が例のアーカイブ・サイトにあったので、パラパラと眺めている。こっちは代数・解析篇で、もう一冊、幾何篇があるみたい。日本語訳はたしか全部で4冊だったかな。明倫館で眺めただけだが。

とりあえず、しばらくは楽しめそう。付録に e と π が超越数であることの証明が載っているが、どういう方針で矛盾を導くのかを最初にかなり詳しく説明してある。証明そのものは、ヒルベルトによって簡易化されたバージョンということだが、もともとのエルミートのアイディアなどを含めて、丁寧に説明されていて、とても分かりやすい。うーん、素晴しい。

投稿者 sukarabe : 10:01 | この記事の固定URI | コメント (2) | トラックバック (0)

2006年12月25日（月曜日）

サーモンの高次平面曲線 [ 数学 ]

以前、ミシガン大学のサイトから20ページ単位で苦労してダウンロードした(だって一括ダウンロードできないもの・・・) George Salmon の A Treatise on the Higher Plane Curves であるが、もっと手軽に入手できるようになっていた。

一つは復刻版。amazon.comで調べると
Amazon.com: A Treatise on the Higher Plane Curves: Intended as a Sequel to a Treatise on Conic Sections: Books: George Salmon
というものがあった。前に随分と探したのに、これは気付かなかった。復刻年度は2001年となっているのに・・・orz
PDFで持っていても、やっぱり製本されているものが欲しい。うーむ。

もう一つは、Internet Archive (インターネット書庫？)なるサイトで見つけたもの。検索していて見つけたサイトなのだが、こんなサイトがあったとは！著作権の切れた古い書籍(だけじゃないけど)が沢山収録されているみたいだ。おまけに、丸ごとダウンロードできるし、ファイル形式もPDFの他にDJVUなどいろいろ選べるのが嬉しい。

さて、サーモンの本は
Internet Archive: Details: A treatise on the higher plane curves: intended as a sequel to A treatise on conic sections
にある。ただし、初版ではなく第3版。探せば初版も見つかるかもだが。

どうやらあちこちの大学が協力してデジタル化して提供している様子だが、こういう恩恵にあずかれるというのもインターネットのおかげではある。ありがたや、ありがたや。

投稿者 sukarabe : 10:44 | この記事の固定URI | コメント (0) | トラックバック (0)

2006年12月22日（金曜日）

マンフォードの講義録が翻訳されていた！ [ 数学 ]

２、３日前月曜日に本屋でマンフォードの講義録、通称Red Bookとか言われていた代数幾何(スキーム論)の入門講義、の翻訳を見つけた。奥付を見ると出たばかりみたい。うーむ、これの和訳が出版されるとは・・・。

シュプリンガー版以前の謄写版(？)のを持っているのだが、このようにきちんと印刷されてハードカバーで出版されると、原書のもっていたカジュアルな講義録という印象とは違って、何というか、ものすごいtreatiseみたいで、若干違和感を覚えるなあ。そうそう、原書は図版は手書きだったんだよな。

Mumfordと言えば、スキームじゃない方の入門書(Algebraic Geometry I : Complex Projective Varieties、代数幾何学I：複素射影多様体) もあるのだが、こっちも翻訳出してくれると嬉しいなあ。

投稿者 sukarabe : 10:55 | この記事の固定URI | コメント (0) | トラックバック (0)

2006年12月06日（水曜日）

何とタクシーに１７２９が！ [ 数学 ]

先日かみさんと池袋からタクシーで帰ったときの話。荷物が多かったし、かみさん、足が痛いって言うもので。タクシーから降りて、ふと車体を見ると、何と１７２９と！

どうやらその会社での登録番号か何かのようで、車のナンバープレートではないのだが、それにしても１７２９とは何たる偶然！

1729とはハーディーが入院中のラマヌジャンを見舞いに行った時のタクシーの番号。あまり素敵な数ではないな、というハーディーにラマヌジャンが反応する。とても素晴しい数ですよ、二通りに立方数の和で表される最小の自然数です、と。つまり、
$1729=10^3+9^3=12^3+1^3$
ということですね。ラマヌジャンにまつわるエピソードの中でもこの話はピカイチ。ああ、写真撮っとくんだったなあ～。残念(笑)。

投稿者 sukarabe : 14:43 | この記事の固定URI | コメント (1) | トラックバック (0)

2006年11月25日（土曜日）

ある期待値の問題(４) [ 数学 ]

以前、この問題の離散近似バージョンを作ったことがあるのだが、X+Yの密度関数がconvolutionになることに示唆されて、離散バージョンの別の解法を思いついた。

$n$ を正の整数として、 $n$ 個の数 $\frac{1}{n}$ , $\frac{2}{n}$ , $\ldots$ , $\frac{n}{n}$ からランダムに一つの数を選ぶ操作を考える。この操作を繰り返すとき、引いた数の和が初めて1を超えるまでの回数の期待値を求めよ、というのが離散近似バージョンになる。

連続バージョンからのアナロジーにより、 $1\leq k\leq n$ なる整数 $k$ に対して、最初の $r$ 回の和が $\frac{k}{r}$ 以下となる確率 $q_r(k)$ を考える。ここで、 $i$ 回目に引いた数を表す確率変数を $X_i$ とすれば、まず、
$q_1(k)=P\left( X_1\leq \frac{k}{n} \right) = \frac{k}{n}$
となる。次に、
$q_2(k)=P\left( X_1+X_2 \leq \frac{k}{n} \right) =\sum_{j=1}^{k} \frac{1}{n}\cdot\frac{k-j}{n} =\frac{k(k-1)}{2n^2}$
となる。ここで、離散変数についてのコンボリューションが出てきている。これを繰り返すと、一般に
$q_r(k)=P\left( X_1+X_2+\cdots+X_r \leq \frac{k}{n} \right) = \frac{_k{\rm C}_r}{n^r}$
となるだろう。多分・・・。ちゃんと計算してないけど、パスカルの三角形の性質から階差に書けるから、帰納法で示せると思う。

すると、これも連続バージョンと同様に、和が初めて $\frac{k}{n}$ を超えるまでの回数の期待値 $E(k)$ は
$E(k)=\sum \frac{_k{\rm C}_r}{n^r} = \left(1+\frac{1}{n} \right)^{k}$
のようになるのではなかろうか。だんだん自信なくなってきた(苦笑)。いや、 $k=n$ の場合、つまり、初めて和が１を超えるまでの回数の期待値が
$\left(1+\frac{1}{n} \right)^{n}$
になることは別の方法でチェック済みなのであるが。

投稿者 sukarabe : 15:36 | この記事の固定URI | コメント (0) | トラックバック (0)

2006年11月23日（木曜日）

確率と合成積(畳み込み) [ 数学 ]

日記を書きながら、やっと次の事を認識した。つまり、確率変数 $X$ , $Y$ があり、それぞれの確率密度関数が $f$ , $g$ であるとする。このとき、 $X+Y$ の密度関数はコンボリューション(合成積、畳み込み)
$(f \ast g)(x)=\int f(x-t)g(t)\,dt$
で与えられる、ということ。 $X$ と $Y$ は独立じゃないと駄目なんだろうなあ、やっぱり。

これですべて氷解した(笑)。そうか、そういうことだったのね。しかし、こんな基本的な事すら今まで知らなかったなんて！(汗)

投稿者 sukarabe : 11:11 | この記事の固定URI | コメント (0) | トラックバック (0)

ある期待値の問題(３) [ 数学 ]

０から１までの実数をランダムに選ぶので、確率密度関数は $f(x)=1$ になる。 $x$ 以下の実数を取り出す確率は
$q_1(x)=\int_0^x f(t)\,dt=x$
となる。２回取り出したときに和が $x$ 以下になる確率 $q_2(x)$ は、
$q_2(x)=\int_0^x f(t)q_1(x-t)\,dt=\frac{x^2}{2}$
以下同様にして、n回までの和が $x$ 以下になる確率 $q_n(x)$ は
$q_n(x)=\int_0^x f(t)q_{n-1}(x-t)\,dt=\frac{x^n}{n!}$
となるだろう。ホントかな？ちょっと自信ない(苦笑)。まあ、あってるとして続けると、和が $x$ を超えるまでの回数の期待値 $E(x)$ は、
$E(x)=1+x+\frac{x^2}{2}+\cdots+\frac{x^n}{n!}+\cdots=e^x$
となる。

投稿者 sukarabe : 09:12 | この記事の固定URI | コメント (0) | トラックバック (0)

2006年11月22日（水曜日）

ある期待値の問題(２) [ 数学 ]

０から１までの数字をランダムに選んだとき、n回で初めて和が $x$ を超える確率を $p_n(x)$ とする。一方、n回までの和が $x$ を超えない確率を $q_n(x)$ とする。すると、
$p_n(x)=(1-q_n(x))-(1-q_{n-1}(x))=q_{n-1}(x)-q_n(x)$
となるから、和が初めて $x$ を超えるまでの回数の期待値 $E(x)$ は
$E(x)=\sum np_n(x)=q_0(x)+q_1(x)+q_2(x)+\cdots=1+q_1(x)+q_2(x)+\cdots$
となる。よって、n回足しても和が $x$ を超えない確率 $q_n(x)$ を求めればよいことになる。多分この方針で解くのが正統派なんだろうな、と思う。何故コンボリューションが現れるかは次回。

投稿者 sukarabe : 19:25 | この記事の固定URI | コメント (0) | トラックバック (0)

ある期待値の問題(１) [ 数学 ]

学生時代に学園祭で質問された問題をふと思い出した。０以上１以下の実数をランダムに選んで足していくとき、何回ではじめて１より大きくなるか、回数の期待値を求めよ、というもの。

確率は苦手なのだが、仕方なく解いた。僕の方法は期待値の関係式を直接作るので、厳密性に欠けるかもだが、概略次の通り。 $x\geq 0$ として、和が $x$ より大きくなるまでの回数の期待値を $E(x)$ とおく。一回目に引いた数字を $t$ とすると、残りは $x-t$ になるから、
$E(x)=1+\int_0^x E(x-t)\,dt$
が成り立つだろう。多分・・・(ちょっと弱気)。あ、 $t<0$ のときに $E(t)=0$ と延長しておく必要があるか・・・。この積分方程式を解けば、 $E(x)=e^x$ となる。よって、 $x=1$ として、 $e=2.7182\cdots$ というのが答え。結果が意外で、しかも自然対数の底がこんなところで！という驚きもあり、へえ～という感じで印象に残っていた。

友人のY氏がきちんとした解答を作っていたのだが、どんなのだったか忘れてしまった。確かコンボリューションが出てきたのだが。うーん・・・。

投稿者 sukarabe : 11:20 | この記事の固定URI | コメント (0) | トラックバック (0)

2006年10月11日（水曜日）

有限群の表現 [ 数学 ]

思い起こせば、大学2年の冬学期にH先生の授業で習ったはずの内容なのであった。何というか抽象的で理解できなかったんだよなあ。理解できなくてもその後、それほど困らなかった(苦笑)ということもあり、是が非でも理解しようと頑張ることもなかった。抽象的な事がすべて苦手ということでもなかった。ホモロジー代数とかはけっこう好きだったし、層(Sheaf, faisceaux)とか層係数コホモロジーとかも嫌いではなかった。ガロア理論も平気。というかガロア理論、全然抽象的じゃないが(笑)。

何故か群の表現論は全然駄目であった。たしか群環(Group Algebra)とかあたりから落ちこぼれた気がする。そんなワタシであったのだが、この度、新内閣の精神に則り、再チャレンジしてみたいと思う(笑)。

で、すごく初歩的な話。「連続群論」と平行して、同じ杉浦先生の「応用数学者のための代数学」(岩波書店)というのを読んでいるのだが、情けなくなるくらい初歩のところで感激(苦笑)。おお、こんな事だったのか、と。いや、書くのが恥ずかしいのであったが。

3次対称群 $S_3$ を考える。置換(231)に行列 $\left(\begin{array}0&1&0\\0&0&1\\1&0&0\end{array}\right)$ を対応させる、といった感じで、 $S_3$ から $GL_3(\mathbb{C})$ への準同型写像を作る。要点は置換に対応して $\mathbb{C}^3$ の標準基底 $e_1$ , $e_2$ , $e_3$ の置換をするということ。そうすると、これは中への同型になる。つまり忠実な表現ということになる。なんだ、簡単じゃあないかぁ(笑)。というか、この行列表現、うすうす知っていたなあ、と。

この表現を $\rho$ で表す。 $e_1+e_2+e_3=\left(\begin{array}1\\1\\1\end{array}\right)$ で張られる空間は、明らかにこの表現の不変部分空間になっている。そこで、その空間とそれに直交する空間に分解すれば、表現 $\rho$ は $\rho=\rho_1\oplus\rho_2$ と直和分解される。ここで、 $\rho_1$ は１次の恒等表現、 $\rho_2$ は2次の表現で、いずれも既約になる。これで、 $S_3$ の既約表現が二つ得られたことになる。 $e_1+e_2+e_3$ を含む正規直交基底を作って、それに関する $\rho_2$ の行列表現をすると、(基底の取り方にもよるが)、例えば互換(12), (13)は、それぞれ、
$\left(\begin{array}-\frac12&\frac{\sqrt3}{2}\\ \frac{\sqrt3}{2}&\frac12\end{array}\right), \qquad \left(\begin{array}-\frac12&-\frac{\sqrt3}{2}\\ -\frac{\sqrt3}{2}&\frac12\end{array}\right)$
になる。これって線対称移動じゃないか！へえ～、なのである。

$\rho_1$ , $\rho_2$ の他に交代表現もあるから、全部で3個の既約表現が得られたことになる。これで $S_3$ の既約表現は尽くされるらしいのだが、その証明は、もっと先まで読まないと分からないらしい。

ということでページをめくってみると・・・げげげ！やはり群環(群多元環)が(大笑)。ああ、やっぱりいらっしゃったのね、トホホ。

投稿者 sukarabe : 17:49 | この記事の固定URI | コメント (15) | トラックバック (0)

2006年09月13日（水曜日）

「連続群論入門」は良い！ [ 数学 ]

こんなことならもっと早く読んでおけば良かった(苦笑)、と、山内・杉浦「連続群論入門」を読みながら思う、orz... まあ興味がないときに無理やり読んでも結局は身に付かないだろうから、早い遅いに関係なく、興味が出てきたときに読むのが一番ではあるが。

まだ第2章の「回転群とその表現」あたりなのだが、それでもいろんな人がほめている事柄がなるほどなあ、とやっと思えるようになった(笑)。線型代数、微分積分、多様体といった教養から学部3年ぐらいまでに学ぶことの格好の応用になっていることが良く分かる。そう思えるのは、SO(3)とSU(2)について具体的に詳しく説明してあるからだ。それに、所々に杉浦先生らしいなあ、と感じる解説があり、楽しい。例えば、62ページには、SU(2)の既約表現をすべて求めることと、完全可約の証明についての方針が書いてある。

・・・このような表現の完全性と表現の完全可約性の証明は表現論の最も重要な論点である。この問題を論ずるのに、全く異なる二通りの方法がある。一つはリー環の表現論によるいわば微分的な方法で、一つは群上の不変積分を用いる積分的方法であり、それぞれ E. Cartan および H. Weyl によって発展させられたものである。この二つの方法は、いずれも非常に興味深いもので、リー群論の最も特長的な論法を示すものであるから、結果の重複をいとわず次節以下で、これを詳しく述べることにする。われわれがここで直接論ずるのは SU(2) または SO(3) という特別な群であるが、ここにおいて論点の本質的な部分は残りなく現われるのであって、一般の (コンパクト半単純リー群の) 場合にも複雑にはなるがほとんど同じ線に沿った議論が成り立つのである。

うーん、思わずこの先を読んでみたいと思ってしまうよねえ(笑)。

投稿者 sukarabe : 09:02 | この記事の固定URI | コメント (3) | トラックバック (0)

2006年09月07日（木曜日）

山内、杉浦「連続群論入門」 [ 数学, 本 ]

部屋の整理をしていると、: 山内恭彦、杉浦光夫共著の「連続群論入門」が出てきた。恥ずかしながら表現論はほとんど知らない。というか興味がなかった。今でもそれほど興味があるわけではないが、通勤の友としてこれを携帯することにした。小冊子の入門書なのに、かなりの内容がある。

杉浦先生の本はどれもそうだが、この本も丁寧で内容豊富。今日は、AdjointによりSO(3)とSU(2)がほとんど同じこと(つまり上への準同型で、Kernelが1と-1になること)と、Adjointが複素平面の１次分数変換とリーマン球面の回転を結び付けていることを理解した。非常に満足。計算をフォローするのが通勤では難しいのだが、なんとか最後まで読みたいと思う。

投稿者 sukarabe : 22:24 | この記事の固定URI | コメント (2) | トラックバック (1)

2006年08月29日（火曜日）

ステキだったのはつかのま [ 数学 ]

つい誘惑に負けて考えてしまった。というか、図を描いているうちに出来てしまった。ああ、よせばよかった。こんなに簡単とは。いや、簡単でも美しいと思えることもある。これは・・・ううむ、微妙だ。美しいと思えないわけではない。でも、第一印象はあんなにステキだったのに、と思うと残念。

しかし、なんだなあ。美しいものは眺めるに如かずであろうか。数学に限らず(自爆)。

投稿者 sukarabe : 11:33 | この記事の固定URI | コメント (0) | トラックバック (0)

2006年08月28日（月曜日）

ちょっとステキな折り紙の問題 [ 数学 ]

傑作というよりは佳作という感じなんだろうが、次のようなステキな問題がKömalのサイトにあった。長方形の折り紙をまず半分に折って折り目を付け、次に図のように一つの頂点が先ほどの折り目の上に重なるように折り曲げる。

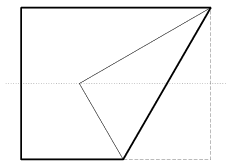
このとき、右上の鋭角は正確に60°になっていることを証明せよ。

何よりもまず結果が美しい。それに意外性がある。不思議だなあと証明を考える時間が楽しい。証明ができてしまうと神秘性がなくなって、かえってつまらなく感じてしまったりする。だから、まだ証明は考えないでおこう(笑)。

投稿者 sukarabe : 23:27 | この記事の固定URI | コメント (0) | トラックバック (0)

2006年08月16日（水曜日）

素敵な幾何の問題 [ 数学 ]

偶然にこんな問題を知った。頂角Aが20°である二等辺三角形ABCがある。辺AC上に、AD=BCとなる点Dをとる。このとき、∠ADBは何度か？あそびやせんとさんのサイトに問題と解答が載っています。

全体に例の問題に似た雰囲気だったので、正三角形を作ることは何となく予想していたのだけど、このように外側に作るとは思いもよらなかった！いや、久々に感動しました。それにしても、すっきりした解答です。素晴しい～。

投稿者 sukarabe : 14:59 | この記事の固定URI | コメント (0) | トラックバック (0)

2006年08月06日（日曜日）

シンプルな例題 [ 数学 ]

備忘録。 $\lim_{n\to\infty}\left(\sum_{k=1}^{n}\frac{1}{{}_n{\rm C}{}_{k}}\right)^{n}$ はさすがに粉飾が酷すぎるかも、ということで、よりシンプルな例題を。

とりあえず、こんな感じでどうだろうか。
$\lim_{n\to\infty}\left(1+\frac{2}{n}+\frac{3}{n^2}+\cdots+\frac{n}{n^{n-1}}\right)^n$

投稿者 sukarabe : 08:28 | この記事の固定URI | コメント (0) | トラックバック (0)

2006年06月26日（月曜日）

答え [ 数学 ]

先のエントリーの答え。平方数が一つでも含まれていたら，無数に含まれることを示せばよい。平方数の項があったとすると，そこからスタートすることにすれば，初項が平方数であるとして一般性を失わない。よって，この数列の一般項は $f(n)=a^2+bn$ と表せる。ここで， $a$ , $b$ は自然数。すると $n=2ak+bk^2$ の場合につねに平方数となる。以上で証明終わり。やれやれ，考えて損した(笑)。

投稿者 sukarabe : 21:03 | この記事の固定URI | コメント (0) | トラックバック (0)

2006年06月25日（日曜日）

一瞬、面白いかなと思ったのだが [ 数学 ]

ネット散策中に偶然見つけた問題。一瞬、とんでもなく難しいのでは、と思ったが、３分ほど考えたら、実に簡単であることが分かった。

自然数からなる等差数列がある。このとき、この等差数列の項の中に平方数はまったく現れないか、あるいは無数にあるかのいずれかであることを証明せよ。

簡単でも面白い問題はあるが、これはねえ。解けてしまうと、実にくだらない(笑)。

投稿者 sukarabe : 18:31 | この記事の固定URI | コメント (0) | トラックバック (0)

2006年06月20日（火曜日）

MaximaとTeXmacsをVAIOにインストール [ 数学 ]

一応Macintoshの方にはMaximaをインストールしてあるのだが、VAIOの方にもインストールしてみた。さすがにユーザーが多いのでWindows版の方が、いろいろと便利になっているような気がするなあ。

次のページがとても参考になった。
http://physics.s.chiba-u.ac.jp/~kurasawa/index.html#Maxima
数式処理システムMaximaで楽をしよう

先にMaximaをインストールしてからTeXmacsをインストールすると、Maximaの場所を自動で調べてくれるみたい。まあ、自分でパスを記述するほうが性にあっているのだが。さっそく、ノコギリ歯関数 $y=\frac{\pi-x}{2}$ のフーリエ展開のグラフなんぞを描かせてみた。この場合、
$\frac{\pi-x}{2}=\sin x+\frac{\sin 2x}{2}+\frac{\sin 3x}{3}+\frac{\sin 4x}{4}+\cdots \qquad (0<x<2\pi)$
となるのだが、例えば、第５項までのグラフを描かせるには、
plot2d(sin(x)+(sin(2*x))/2+(sin(3*x))/3+(sin(4*x))/4+(sin(5*x))/5, [x,0,2*%pi]);
という命令を入力すればよい。Gnuplotを取り込んでいるらしく、maximaをインストールするだけで、グラフも描けるようだ。おお、素晴しい。

投稿者 sukarabe : 15:48 | この記事の固定URI | コメント (0) | トラックバック (0)

2006年06月17日（土曜日）

クーラン・ヒルベルト第２巻 [ 数学 ]

リチャード・クーラント(Richard Courant, 英語読み) の伝記「クーラント」(原題は、Courant in Göttingen and New York) を読んでいたら、クーラン・ヒルベルト(Courant-Hilbert)「数理物理学の方法」の第２巻(原書の場合、日本語訳では第３巻と第４巻になる)のことについてあれこれ書かれていたので、ちょっとだけ斜め読み。

実のところ、有名な本ではあるが、ちゃんと読んだことなし(苦笑)。第２巻のテーマである偏微分方程式の理論は、シュワルツの超関数や関数解析ができてから様変わりしているので、いまさらクーラン・ヒルベルトを読むのもなあ、とは思ったかも。

しかし、ざっと眺めてみると、なかなか楽しそうな感じ。やっぱり過度に抽象化された数学は疲れる。それに正直に言うと、関数解析とか嫌い(笑)。クーラントの本は古典解析のかほりがして、今だったら読んでみるかという気にさせる。

それに、最後の方にプラトー問題について、短くはあるが解説が載っている。プラトー問題については、クーラントが素人向けに書いた本「数学とは何か」で読んだことがある。うかつなことに、伝記を読むまでクーラントがプラトー問題をディリクレの原理に帰着させて解いていたことを知らなかった。プラトー問題自体はダグラスによって初めて解かれたのだが、クーラントはその解法(別の変分問題に帰着させる)が気に入らず、より直接的な解法を得たのだという。それだけ愛着のある話題であるからこそ、素人向けの本にまで書くわけだ。クーラン・ヒルベルトの本の方には、ダグラスとの悶着など(先取権に関しての)は一切触れておらず、ただ「プラトー問題は、ラドーとダグラスによって初めて解かれた。ここの解説は、クーラントの論文、・・・・・に拠る」という脚注があるのみ。

ということで、暇ができたら、少しずつ読んでみたいと思う。思うのだがね・・・。

投稿者 sukarabe : 15:29 | この記事の固定URI | コメント (0) | トラックバック (1)

2006年06月04日（日曜日）

整数パズル [ 数学 ]

以前、どこかで見つけた問題。出典は不明。「連続した2つの自然数の立方の差がたまたまある自然数の平方に等しくなっていたとする。このとき、その自然数は、連続した2つの自然数の平方の和として表すことができる」というもの。
$8^3-7^3=169=13^2$
がそういう場合。このとき、確かに $13=2^2+3^2$ となっている。式で書くと次のようになる。
$(m+1)^3-m^3=N^2$
であるときは、 $N=k^2+(k+1)^2$ と表される。

以下の証明は短いが、いささかトリッキーかも。もっと自然な証明が欲しいが・・・。

仮定から、
$3m^2+3m+1=N^2$
となるが、これを次のようにペル方程式の形へと変形する。平方完成して・・・
$\begin{eqnarray} 3\left(m+\frac{1}{2}\right)^2+\frac{1}{4}&=N^2 \\ 3(2m+1)^2+1&=(2N)^2 \end{eqnarray}$
そして、定数項を移項して因数分解する。
$3(2m+1)^2=(2N+1)(2N-1)$
ここで、ユークリッドの互除法などにより、 $2N+1$ と $2N-1$ は互いに素であることがわかるから、
$2N+1=x^2, \quad 2N-1=3y^2$
あるいは、
$2N+1=3x^2, \quad 2N-1=y^2$
となる。ここで、前者の場合、 $x^2=3y^2+2$ となり、3で割った余りを考えると直ちに矛盾が出る。つまり、この場合はあり得ない。よって、後者の場合に限るが、 $y$ は奇数となるので、 $y=2k+1$ と置けば、
$N=2k^2+2k+1=k^2+(k+1)^2$
となる。これで証明されたことになる。

投稿者 sukarabe : 14:09 | この記事の固定URI | コメント (0) | トラックバック (0)

2006年05月07日（日曜日）

２のベキ乗 [ 数学 ]

面白い問題はレベルとは関係なくあるなあ、と改めて実感させられたのが次の問題。最近、友人が教えてくれたもの。2の何乗でも良いのだが、例えば2の1000乗を考える。関数電卓で計算させると、
$2^{1000}=1.071508\cdots \times 10^{301}$
と表示される。これから、2の1000乗は302桁の数であり、その最高位の数字(一番左側の数字)は1であることが分かる。では、2の1乗、2の2乗、2の3乗、・・・、2の1000乗の1000個の数のうち、最高位の数字が4であるものは、一体何個あるでしょうか。

中学生でも解けるこの問題だが、個人的にはちょっと悔しい。随分前になるが、2のベキ乗ネタでは問題を作ったことがある。それは知られていた結果だったのだが(あとで分かった)、個人的には気に入っていたのだった。上の問題はネタ的に、その問題のすぐ近所にあるのだ。うーん、この問題を思いつかなかったのは、とっても悔しいのである。いや、脱帽しました。

投稿者 sukarabe : 22:17 | この記事の固定URI | コメント (2) | トラックバック (0)

2006年03月23日（木曜日）

自然数の累乗和に関する等式 [ 数学 ]

ちょっと前に自然数の累乗和(ベキ和) $1^p+2^p+3^p+\cdots+N^p$ に関連したある恒等式を知ったのだが、たまたま実家で本棚にあったMax Koecher(マックス・ケッヒャー)著の「数論的古典解析」(この邦題はちょっとどうかと思うが・・・原題は Klassiche elementare Analysis) をながめていたら(第6章のベルヌーイ多項式の部分)、ちょうど同じ等式が練習問題に載っていた。
$s_{p}(N)=\sum_{k=1}^{N}k^p=1^p+2^p+3^p+\cdots+N^p$
と書くときに等式
$\sum_{0\leq k\leq \frac{1}{2}(p-1)} $\array{p\\ 2k+1}$ s_{2p-2k-1}(N)=\frac{1}{2}N^p(N+1)^p$
が成り立つというもので、出典はMathematical Gazette 誌の第42巻(1958年)とあった。ここで記号 $\array{p\\ 2k+1}$ は異なる $p$ 個から $(2k+1)$ 個を選ぶ選び方の数を表すもので、要するに組合せの数(2項係数)のこと。

証明は難しくないが(両辺の階差を取れば等しいことが直ぐに分かる)、なかなか興味深い式。高校の教科書などには、 $s_{p}(N)$ を求めるのに2項定理を用いて $p$ を一つずつ増やしていく方法が紹介されていて、それは有名だと思うが、上記に等式によれば $p$ が奇数の場合の $s_p(N)$ は偶数の場合を経由することなく求めることができる。つまり、1乗、3乗の累乗和が分かれば、次は直接5乗の和が計算されることになる。ま、そういう実用上の問題は別にしても美しい式には違いない。

投稿者 sukarabe : 09:44 | この記事の固定URI | コメント (0) | トラックバック (0)

2006年02月13日（月曜日）

とある三角関数の公式 [ 数学 ]

Sa氏から教わったのだが、
$\cos^{n}\,x=\frac{1}{2^n}\sum_{k=0}^{n} {\,}_{n}{\rm C}_{k}\,\cos(n-2k)x$
という等式が成り立つらしい。証明は(複素数を用いると)難しくないが、こんな初等的な範囲でも知らないことがまだまだあるんだなあ、と痛感。

投稿者 sukarabe : 09:04 | この記事の固定URI | コメント (0) | トラックバック (0)

2006年02月01日（水曜日）

微分方程式と連分数 [ 数学 ]

ジーゲルの「超越数」の第2章の冒頭に、ルジャンドル(Legendre)がランベルト(Lambert)の研究を一般化して、2階の微分方程式を満たす無限級数を考えて連分数展開を導いた、という事が書かれている。そこで、ランベルトの結果の再現を試みた。

考える関数は双曲線関数を変形したもので、
$f(x)=\cosh (2\sqrt{x})=1+\frac{2^2}{2!}x+\frac{2^4}{4!}x^2+\frac{2^6}{6!}x^3+\cdots$
これは、合流型の超幾何級数(たしかそうだと思うが記憶があやふや)の特殊な場合で、微分方程式
$x\frac{d^2y}{dx^2}+\frac{1}{2}\,\frac{dy}{dx}=y$
の解になっている。この微分方程式の両辺をn回微分して、 $A_n(x)=\frac{ 2y^{(n)}}{ y^{(n+1)}}$ と置けば、再帰公式
$A_n(x)=2n+1+\frac{ 4x}{ A_{n+1}(x)}$
を得る。 $A_0(x)=\frac{ 2\sqrt{x}\cosh(2\sqrt{x})}{\sinh(2\sqrt{x})}$ であるから、この式の連分数展開が得られたことになる。式を美しくするために、 $x$ のところに $\frac{ x^2}{4}$ を代入すると、
$\frac{ x(e^x+e^{-x})}{ e^x-e^{-x}}=1+\frac{ x^2}{ 3+\frac{ x^2}{ 5+\frac{ x^2}{ 7+\cdots}}}$
となる。ランベルトの連分数の形にするには、さらに逆数をとり、 $x$ を掛ければよい。

さて、 $x=1$ と置いてみよう。
$\frac{ e^2+1}{ e^2-1}=1+\frac{ 1}{ 3+\frac{ 1}{ 5+\frac{ 1}{ 7+\frac{ 1}{\ddots}}}}$
となる。美しい！そうは思いませんか？

投稿者 sukarabe : 08:42 | この記事の固定URI | コメント (0) | トラックバック (0)

2006年01月17日（火曜日）

eに関連した連分数 [ 数学 ]

先日書いた $e$ の連分数展開に関連して、少しだけ。

$e$ の連分数展開は、周期性はないものの3つ毎にパターンがあった。そのため、第 $n$ 近似分数( $n$ -th convergent)を3つ毎にピックアップした数列が単純な漸化式を満たし、それが本質的には $T_{n}=\int_0^1 \frac{t^n(t-1)^n}{n!}e^t\,dt$ と一致している、というのが証明の粗筋であった。

してみると、 $T_n$ だけでも $e$ の連分数を縮約(？)したものを表せそうじゃないか、と思える。 $T_n$ は $n$ の偶奇によって符号が変わるため、つねに正の値を取る積分
$I_{n}=\int_0^1 \frac{t^n(1-t)^n}{n!}e^t\,dt$
に取り替えて考える。単に、 $t-1$ を $1-t$ にしただけ。これは、次の漸化式を満たす。
$I_n=2(2n+3)I_{n+1}+I_{n+2}$
そこで、両辺を $I_{n+1}$ で割れば、
$\frac{I_n}{I_{n+1}}=2(2n+3)+\frac{1}{ \frac{I_{n+1}}{I_{n+2}} }$
となる。あとは、これを繰り返せば、連分数の出来上がりというわけ。

$I_0=e-1$ , $I_1=3-e$ なので、最終結果は次となる。
$\frac{e-1}{3-e}=6+\frac{1}{ 10+\frac{1}{ 14+\frac{1}{ 18+\frac{1}{ \ddots} } } }$
連分数の形は、等差数列となり美しいが、値の方はイマイチかあ〜(苦笑)。残念！？

投稿者 sukarabe : 14:14 | この記事の固定URI | コメント (0) | トラックバック (0)

2006年01月15日（日曜日）

eの連分数展開 [ 数学 ]

自然対数の底 $e=2.71828\cdots$ は不思議なことに規則的な連分数展開を持つ。
$e=2+\frac{1}{ 1+\frac{1}{ 2+\frac{1}{ 1+\frac{1}{ 1+\frac{1}{ 4+\frac{1}{ 1+\frac{1}{ 1+\frac{1}{ 6+\frac{1}{ 1+\frac{1}{ 1+\frac{1}{ 8+\frac{1}{\ddots}}}}}}}}}}}}$
これを発見したのは、例によってEuler(オイラー)だったかな？Eulerが証明したかどうかは知らない。 [追記：Eulerは証明もしていたようだ。] Courant-Robbinsの「数学とは何か」で見て以来、気になっている等式なのだが、証明が載っている本は少ない。自分が知っている証明の中では、級数や関数の連分数展開から導く方法が自然であり、好きなのであるが、より初等的で短い証明を偶然見つけたので備忘録として記録しておこう。

見つけたのは、William Steinという方のサイト。ハーバード大での講義を元にした初等数論の入門書(PDF版)が置いてあるが、その中にあった。次のページからダウンロードできる。
William Stein : Elementary Number Theory

証明のポイントは、上記の連分数の第n近似分数の分子・分母が満たす漸化式が、積分
$T_{n}=\int_{0}^{1} \frac{t^{n}(t-1)^{n}}{n!} e^{t} \,dt$
が満たす漸化式
$T_{n}=2(2n-1)T_{n-1}+T_{n-2}$
と本質的に同じというか帰着できることにある。この証明は、Henry Cohnという方によるもので、表現方法を少し変えたものであると書いてある。そのページに行くと、一番下に、当該のファイルがある(PSとPDFと両方の版)。PDFはフォントの埋め込みのせいか読みにくかったので、PSをPDFに変換して読んでみた。すると、この証明のアイディアはエルミートが $e$ の超越性を証明したときの副産物であり、それを整理・簡略化したものである旨の説明があった。追跡はここまで。エルミートの論文は全集にあたらないとだめかあ。

投稿者 sukarabe : 17:28 | この記事の固定URI | コメント (0) | トラックバック (0)

2006年01月13日（金曜日）

ジーゲルの「超越数」 [ 数学 ]

ジーゲル(Carl Ludwig Siegel)の本は日本語訳を出版できなかったと思う。なんでもジーゲルが、自分が理解できない言語への翻訳を拒否しているという話だった。勘違いしているかもしれないが。ということで、私家版が密かに(？)流通したりするのであった。本棚を整理していたら、ジーゲルの「超越数」の翻訳が出てきた。もうかなり前に某先生からもらったもの。学生のときに自分で訳して印刷されたらしい。なんてったって、わら半紙にガリ版刷りですからね。時代が分かろうというもの(笑)。

内容は、自然対数の底 $e=2.7182\cdots$ が無理数であることの証明から始まって、最後はGelfond-Schneiderの定理( $2^{\sqrt{2}}$ が超越数であることなど)まで、ゆったりとした感じで進む。先を急ぐというよりは、あちこちきれいな風景を眺めながら気が付くと山頂に着いていたという感じ。例えば、 $e^x$ の無限級数展開を用いて $e$ が無理数であることを証明したあと、その流れで $e$ が2次の無理数でないこと(つまり、どんな整数 $a$ , $b$ , $c$ に対しても、 $e$ が2次方程式 $ax^2+bx+c=0$ の解にならないこと)の簡単な証明が載っている。どうせ後で $e$ が超越数であることを証明するのだから、なくても構わないのだが、その証明法がちょっと素敵だったりする。ジーゲルの本や講義録には、このように悠然としたところがあるのだ。いいよなあ〜。

投稿者 sukarabe : 19:08 | この記事の固定URI | コメント (0) | トラックバック (0)

2005年12月19日（月曜日）

イプシロン・デルタ(3) [ 数学 ]

この話題を書くきっかけとなったのはcalc氏の日記なのだが，いろいろ調べてみると，コーシーが一様収束の概念に到達できなかったのも仕方ないと思える。コーシーの功績というものは，つまるところ「極限の概念」を微積分の基礎に置いたことなのだ。ライプニッツのように $dx$ を「無限小という量」として扱うようなことでは説明できないことが多々あり，確実な基礎付けが望まれていた時期でもあった。そういうわけでコーシーは極限の概念を基礎として微分積分学を再構築した。したのだが，極限の定義はやや直感的でありイプシロン・デルタほどの徹底的に厳密化されたものではなかった。そのため，議論の細部においてときおり誤った議論をしているようだ。直感的な定義の弱点は関数列の極限で顕著に表れる。関数列 $f_n(x)$ が関数 $g(x)$ に収束するとはどういうことか？ $x$ を固定すれは数列の極限だが， $x$ が変化するとどうなるか？このあたりを明確に表記するにはイプシロン・デルタの記法が不可欠(というのは言い過ぎかもだが)である。

$x$ の変化が問題になるのは連続性の定義でも起こる。各点での連続性における $\delta$ が $x$ に依存せずに選べるときは「一様連続」というのであるが，コーシーはこの一様連続の概念にも到達していない。それも無理からぬことだと思う。コーシーは連続関数が積分可能であることの(不完全な)証明を与えているが，その証明では閉区間において連続な関数があたかも一様連続であるかのように処理されている。つまり $\delta$ が閉区間のどこでも通用するようにとれると錯覚している。結果的に正しいのだが，このことは決して自明ではない。正しい証明はハイネによって与えられた。(それがハイネ自身によるものか，あるいはワイエルシュトラスによるものかは不明であるが。)

ということで，単なる数列の極限と違って，関数列の極限はかくもデリケートで難しいということですねえ。関数解析を学ぶと関数空間における点列の極限になってしまい，逆にどこが難しいのか分からなくなってしまう(笑)のだが，これが進歩というものかもしれない。そう言えば高木貞治の本に書いてあったなあ。「数学に王道なしというが，実は既成数学は王道である」と。

投稿者 sukarabe : 11:08 | この記事の固定URI | コメント (0) | トラックバック (0)

2005年12月07日（水曜日）

物理の人が書く数学の教科書 [ 数学 ]

以前本屋で「理工学者が書いた数学の本」とかいうシリーズを見かけたことがある。ふーんと思って立ち読みしたが，正直言ってつまらなかった。案外と几帳面で数学の人が書くのと大差ないように感じたものだった。さて，偶然にWebで公開されている「物理の人による数学の教科書」を発見した。実際には講義ノートらしく草稿ということだが，なかなかの完成度でけっこう楽しめた。
学習院大学理学部物理学科の田崎晴明さんによる数学の本のページ

おすすめは10章のベクトル解析ということなので，そこからざっとながめてみた。具体的な計算例が電磁気などの物理から採られているのと，ざっくばらんな口調で心地良く読める。定義を天下りにするのではなく，物理現象と絡めて導入していく立場は素晴らしいと思う。他の章も読んでみた。ちょっと驚いたのだが，イプシロン・デルタとかコーシー列とか，基礎的なこともけっこう詳しく書いてある。物理の人がこの辺りを丁寧に書かれるとは予想外だった。イプシロン・デルタの部分で，「ほしたら，精度 ε=0.00001 やったらどないや？」「いけずやなあ，それやったら N=3500や!」というくだりには笑った。遠山啓の「数学入門」では(落語「浮世根問」の)御隠居と八さんの掛け合いだが，たしかに関西弁は感じが出ている。

投稿者 sukarabe : 16:38 | この記事の固定URI | コメント (0) | トラックバック (0)

2005年12月06日（火曜日）

イプシロン・デルタ(2) [ 数学 ]

本棚を探すと，安倍齊(ひとし)著「微積分の歩んだ道」(森北出版)があった。コーシーに関して次の記述がある。

ライプニッツ以来， $dx$ は「極めて小さい固定された量」を表していたが，コーシーは「 $dx$ は変量を表し，0にいかほどでも近づく変量である」と定義し，無限小の概念をまず明確にした。次に連続の概念を次のように定義した。
“いま $f(x)$ が与えられ， $f(x)$ は $x$ と共に変化するものとする。次に， $x$ とは別に，無限に小さい変化する量 $\alpha$ が与えられ，次の2つの量の差
$f(x+\alpha)-f(x)$
が， $\alpha$ が無限に0に近づくとき，いかほどでも小さくなるならば，「 $f(x)$ は $x$ で連続である」という。”
現代流に言えば「 $\alpha$ が0に近づけば $f(x+\alpha)-f(x)$ は0に近づく」ということである。「ε−δ法」を用いたワイエルシュトラスの定義が生まれるまでは最も良い定義であったことはいうまでもない。

どこまで原典に当たって書かれているか不明だが，この部分の記述は「数学史 1700ー1900」のそれと一致する。

投稿者 sukarabe : 20:19 | この記事の固定URI | コメント (3) | トラックバック (0)

イプシロン・デルタ(1) [ 数学 ]

イプシロン(ε)，デルタ(δ)というのはギリシャ文字だが，数学では所謂イプシロン・デルタ論法なるものがある。例えば，関数 $f(x)$ が $x=x_0$ で連続であることの定義は次のようになる。
どんな小さな正の数 $\epsilon$ に対しても「 $|x-x_0|\lt\delta$ ならば $|f(x)-f(x_0)|\lt\epsilon$ が成立する」ような $\delta\gt 0$ を選ぶことが可能であれば， $x=x_0$ において $f(x)$ は連続であると定義する。

長い間，この定義はコーシー(Cauchy)が与えたものと思っていた。ところが最近 calc氏の記事に関連して手近にある本を読んでいるのだが，事はそう単純ではないかもしれない。少なくともこの形で定式化したのはワイエルシュトラスなのかもしれない。

極限や連続のきちんとした定義はコーシーによるものだということに関しては大丈夫なのかな？数学史関係の本はあまり持ってないので，こういうときは困る。とりあえず本棚から探し出してきたのは Dieudonné 編の「数学史 1700ー1900」の3巻本。2巻目の第6章「解析学の基礎」(Pierre Dugac)を読んでみた。

「解析学教程」(1821年)において，コーシーはそれまで曖昧に使われていた「無限小」や「無限級数」といったものに確固たる基盤を与えたとされている。例えば「無限小」とは「0を極限とする数列(あるいは関数)」のことと定義する。それまでの「どんな正の数よりも小さい特殊な量」という曖昧な無限小を捨てて「極限」を主軸に据えたのが最大の貢献と言えるだろう。

さて，連続性の定義は次のように与えられているらしい。「関数 $f(x)$ が点 $x$ において連続であるとは，差 $f(x+\alpha)-f(x)$ の絶対値が $\alpha$ のそれとともに限りなく小さくなること」うーん，これでは限りなく小さくなることの定義はどうするんだ(笑)。

投稿者 sukarabe : 16:08 | この記事の固定URI | コメント (2) | トラックバック (0)

2005年12月04日（日曜日）

「博士の愛した数式」が映画化 [ 数学, 映画・ドラマ ]

もうあちこちで宣伝されているが，小川洋子さんの「博士の愛した数式」が映画化されている。
映画「博士の愛した数式」公式サイト

新春第2弾ロードショーとあるが，いつから劇場でやるのかな？ワーナーマイカル板橋も入っているはずだが，サイトにはまだ告知されていない。

Godfrey Harold Hardy (1887 - 1947)

それにしても博士役の俳優さん・・・世間のイメージする老数学者ってこんな感じなのだろうか(苦笑)。もっとはじけた役者さんでも良かったと思う。実在の数学者で言えば写真のG. H. ハーディーとかだと個人的にはピッタリなんだけどな。この写真だとまだまだ鋭すぎるかもだが(笑)。

投稿者 sukarabe : 12:17 | この記事の固定URI | コメント (0) | トラックバック (0)

2005年11月26日（土曜日）

円錐台の体積 [ 数学 ]

円錐の体積が $\frac{1}{3}\pi r^{2}h$ となることは学校で習うが，円錐台は教えないのかな？上の面の半径を $a$ , 下の面の半径を $b$ , 高さを $h$ とすれば，円錐台の体積は，
$\frac{1}{3}\pi(a^2+ab+b^2)h$
となる。子供の頃に通った塾で教わったと思うが，昨日，ある人に「マニアックな公式ですね」と言われてしまった(笑)。

この公式については楽しい記憶がある。第一に因数分解の公式
$a^3-b^3=(a-b)(a^2+ab+b^2)$
を習っていたので，格好の応用問題だったのだ。円錐の体積の式とこの因数分解を合わせると，円錐台の体積の式を導くことができる。

もう一つは，円錐の体積はどうして円柱の体積の $\frac{1}{3}$ 倍になるのか，に関する事。誰しもが疑問に思い，学校の先生は理由を教えてくれない(多分)。塾の先生に尋ねても，たしか「そうなっとるんだ」とか言われたような(笑)。ところが，円錐台の公式を教わったとき，ピンと来たのだ。ここにヒントがあると。

子供なりに次のように考えてみた。円錐の体積が同じ底面と高さをもつ円柱の体積の定数倍になることはもっともらしい。よって，円錐の体積は，ある定数 $C$ により
$C\cdot \pi r^{2}h$
と表されるだろう。すると，円錐台の体積は，
$C\cdot \pi(a^2+ab+b^2)h$
となる。さて，ここが，ポイントだ。円錐台を特殊化すると円錐だけでなく円柱にもなる！そこで $a=b=r$ , つまり半径 $r$ の円柱にしてみると，円柱の体積は
$C\cdot 3\pi r^{2}h$
となる。ところが，これは $\pi r^{2}h$ に一致するはずじゃないか。ということは
$C=\frac{1}{3}$
でなければならない。やったー，バンザイ。

自分の発見にわくわくしたのだったが，まわりの反応が芳しくない(苦笑)。友達に話しても，？？？という状態。当時Blogがあったらなあ。あーすっきりした(笑)。

投稿者 sukarabe : 09:19 | この記事の固定URI | コメント (2) | トラックバック (0)

2005年11月23日（水曜日）

接空間 [ 数学 ]

珍しく(？)数学が書いてある日記を発見した。
ユークリッド空間で起こる接空間、余接空間との同一視（前編） : 南の島で思うこと−タスマニアにて− -北国tv

多様体の接空間の定義は誰しもが一度は悩むところかもしれない。 $\mathbb{R}^n$ に含まれる多様体，例えば3次元ユークリッド空間内の曲面などでは，接平面は直感的に理解できる。しかし，そのままでは一般の多様体には適用できない。

自分の経験では，3年で多様体の授業を受ける前に，教養の段階で(S先生による)多変数の微積分の授業があった。あったのだが，何と接ベクトルの定義は微分作用素によるものだった(笑)。ちなみに3年の多様体の授業(O先生)は超曲面の話から始まった。おい，順序が逆だろう(苦笑)。手元にS先生の講義ノートがないので確認できないのだが，このような形で接ベクトル・接空間を導入したのは，シュバレー(Chevalley)の Theory of Lie Groups が最初という話だったと思う。n次元多様体の接空間は n次元の線型空間であれば何でもOKというわけにはいかない。そのときには理解していなかったが，曲面の場合の自然な拡張になるためには，いわゆる「自然な同型」になってないとダメ。具体的に言えば，多様体の局所座標系をとりかえた場合の接空間の座標の変化が， $\mathbb{R}^n$ に埋め込んだ場合と同じになっている(つまり同種のテンソルになる)必要がある。これも当時は知らなかったが，Chevalleyがこの本を書いた頃は，一般の多様体の定義がきちんとなされていなかったようだ。リーマン面がWeylの本できちんと定義されたように，多様体の基礎付けもChevalleyの本でなされたわけだ。それに伴って，それまでの添え字だらけのテンソル解析は座標を用いない intrinsicな形に変身した。そういう背景を知らないと，このような定義を受け入れることは心理的に難しいのではないか。

当時 Chevalleyの本も読んだのだが(といっても最初の多様体の定義の所だけ)，接ベクトルの定義には納得できなかった記憶がある。ある程度の納得ができたのは，服部晶夫先生の岩波全書の本(これも手元にないのでタイトル忘れたけど，単に「多様体」だったかな？)を読んでから。接ベクトルをその方向に沿った「方向微分」と関連づける説明があったと思う。この説明が一番良かったかなと思う。

今から思うと，こういう定義の妥当性とか必然性とか，そういった説明がもっと欲しかった。もっとも何でもすぐに飲み込める人もいるから，そういう人にはまどろっこしいのだろうが・・・。

投稿者 sukarabe : 09:46 | この記事の固定URI | コメント (5) | トラックバック (1)

2005年11月09日（水曜日）

素数の音楽 [ 数学 ]

昨日，素数の音楽という本を見つけた。数学の本ではないが，数学と数学者にまつわる逸話などが沢山載っている。メインテーマはリーマン予想で，いかに多くの数学者がリーマン予想の虜(とりこ)になったかという話(ちょっとまとめすぎだが)。リーマン予想(Riemann Hypothesis)とは，リーマン・ゼータと呼ばれる関数についての予想。リーマンのゼータ関数 $\zeta(s)$ とは，正の実数 $s$ に対して
$\zeta(s)=\frac{1}{1^s}+\frac{1}{2^s}+\frac{1}{3^s}+\cdots+\frac{1}{n^s}+\cdots$
と無限級数で表されるもの。ゼータ関数は素数の研究で非常に重要な役割を果たす。解析接続という方法で $\zeta(s)$ の定義域を虚数の範囲まで広げて考えるのだが，その零点つまり $\zeta(s)=0$ となる点が，(自明な零点を除けば)すべて $s=\frac{1}{2}+it$ という直線上にあるだろう，というのがリーマン予想。実軸に近い方から数えて，たしか何百億個までは確かにすべてこの直線上に乗っていることが，(コンピュータを使った)計算で示されているそうだ。それでも「すべて」にはほど遠い(笑)。

まだ詳しく読んだわけではないが，案外と正確に書いてあるなあという印象。その代わり文学的趣には欠けるかも。著者はいったい・・・おやまあ，数学者じゃないの(笑)。なるほど，それなら納得が行く。それにしても，こういう本が新潮社から出るとはねえ。

しかし，どこかで読んだ話の寄せ集めのような感じでもある。幾つかの話題は，リトルウッド(J. E. Littlewood)の「数学雑談」(Littlewood's Miscellany)や，ハーディー(G. H. Hardy)の「ラマヌジャン」(Ramanujan:Twelve lectures on subjects suggested by his life and work)などで読んだ記憶がある。でも知らなかった話もけっこうあって楽しかった。セルバーグの素数定理の初等的証明に関しての，エルデーシュとのもめ事の件も，今回初めて詳しいことを知った。

数学をある程度知らなくても楽しめるものなのか分からないのだが，本屋で平積みみたいに置いてあるところをみると，案外と行ける(？)のかもしれない。評判もまずまずのようだ。例えば，
asahi.com：素数の音楽　[著]マーカス・デュ・ソートイ
 今月の新刊採点/2005年10月/素数の音楽
など。

投稿者 sukarabe : 10:16 | この記事の固定URI | コメント (0) | トラックバック (0)

2005年11月06日（日曜日）

ガウス和に向けた準備(4) [ 数学 ]

(2次の)ガウスの和を(符号を除いて)求める計算例。 $p$ は奇素数とする。 $p=2f+1$ とおき，2つの $f$ 項周期
$\eta_0=\zeta^1+\zeta^{g^2}+\zeta^{g^4}+\cdots+\zeta^{g^{2f-2}} \\ \eta_1=\zeta^{g}+\zeta^{g^3}+\zeta^{g^5}+\cdots+\zeta^{g^{2f-1}}$
を考える。ここで $g$ は modulo $p$ での原始根。ガウス和とは， $\eta_0-\eta_1$ に他ならない。計算は， $p=4n+1$ の場合と $p=4n+3$ の場合で少しだけ違う。具体例で，その違いを見てみよう。

まず， $p=4n+3$ の例として， $p=11$ の場合の計算をしてみる。原始根としては $g=2$ がとれる。 $g^k$ ( $0\leq k \leq 9$ ) の剰余を求めると，
$1,2,\quad 4,8,\quad 5,10,\quad 9,7,\quad 3,6$
となる。つまり，平方剰余の全体 $R$ と平方非剰余の全体 $N$ は，
$R=\left\lbrace 1,4,5,9,3 \right\rbrace, \qquad N=\left\lbrace 2,8,10,7,6 \right\rbrace$
である。すると，
$\eta_0=\sum_{\lambda\in R}\zeta^{\lambda}, \qquad \eta_1=\sum_{\lambda\in N}\zeta^{\lambda}$

まず
$\eta_0+\eta_1=\zeta^1+\zeta^2+\cdots+\zeta^{10}=-1$
は明らか。次に，前回導入した $\eta^{(\nu)}$ なる記号を用いると， $\eta_0\eta_1$ の計算は次のようになる。
$\eta_0\eta_1=\eta^{(1+2)}+\eta^{(1+8)}+\eta^{(1+10)}+\eta^{(1+7)}+\eta^{(1+6)}\\ =\eta^{(3)}+\eta^{(9)}+\eta^{(11)}+\eta^{(8)}+\eta^{(7)} \\ =\eta_0+\eta_0+5+\eta_1+\eta_1 \\ =5+2\eta_0+2\eta_1$
ここで注目すべきは，展開したときに $\zeta^{p}=\zeta^{11}=1$ の項が現れることである。これが $p=4n+3$ の場合の特徴。また， $\eta_0$ と $\eta_1$ の係数は等しくなるが，これはどんな $p$ でも成り立つ事柄。そのことは，直接示すこともできるし，あるいは， $\eta_0\eta_1$ が根の変換に対して不変であることから明らか(ガロア理論)ということもできる。まあ，計算主体でやっている趣旨から言えば，直接的な証明の方が良いだろうが。

ともかく，
$\eta_0\eta_1=5+2(\eta_0+\eta_1)=5+2(-1)=3$
となるので， $\eta_0$ , $\eta_1$ は
$x^2+x+3=0$
の根，つまり $x=\frac{-1\pm\sqrt{11}i}{2}$ となる。以上で， $p=11$ の場合のガウスの和が，
$\eta_0-\eta_1=\pm\sqrt{11}i$
と符号を除いて求められた。

投稿者 sukarabe : 08:35 | この記事の固定URI | コメント (0) | トラックバック (0)

2005年11月05日（土曜日）

エジプト分数 [ 数学 ]

何の脈絡もないが，ふと思い出したので，軽い話題を。

小学生の頃に読んだ絵本(？)というか子供向きの図鑑みたいなもので，「図鑑百科・数の世界」というのがあった。たしか矢野健太郎監修とか書いてあったと思う。出版社は小学館かな？ともかく子供向きの気楽な本なのだが，いろいろと楽しい話が載っていた。その中に「エジプト分数」なるものがあった。なんでも古代エジプトでは単位分数(分子が1の分数)が基本というか重要視されていて，一般の分数を単位分数の和で表すことが試みられていたということだった。

そんなのは簡単なことで，例えば， $\frac{2}{5}$ であれば，
$\frac{2}{5}=\frac{1}{5}+\frac{1}{5}$
とすればよいと，誰でも思うだろう。ところが古代エジプト人は，分母が異なる単位分数の和で表すことにこだわったらしい。

うーむ，面白いことを考えるものだ。だから， $\frac{2}{5}$ の場合は，
$\frac{2}{5}=\frac{1}{3}+\frac{1}{15}$
でなくてはならない。こんな感じで，いろんな分数を「分母の異なる単位分数の和で表したもの」が，例のパピルスに記録されているのだそうな。

さて，どうやったらこういう表示ができるのか。ここが面白いところだ。数式で示すことは易しいが，それでは妙味がないし，だいたい小学生には無理だ。次のような解説があったとおもう。

$\frac{2}{5}$ は2個のスイカを5人で分けることと同じである。2個のスイカを，それぞれ3等分すれば， $\frac{1}{3}$ ずつに切り分けられた6個のピースができる。そこで，これを5人に一つずつ配る。この段階で一人あたり $\frac{1}{3}$ 個のスイカを得たことになる。さて，1ピースが残っている。これをさらに5等分する。すると
$\frac{1}{3}\div 5=\frac{1}{15}$
ずつの5ピースができるから，これを5人に配る。以上で，2個のスイカを5人で均等に分けることができた。一人あたりのスイカの量は，
$\frac{1}{3}+\frac{1}{15}$
となったから，これで $\frac{2}{5}$ を単位分数の和に書くことができたことになる。

実際の説明ではスイカを円にたとえて，円を分割する図版などが付いていたので，ずっと分かりやすかったと思う。今の子供達のための，こうした本はあるのだろうか？

投稿者 sukarabe : 12:49 | この記事の固定URI | コメント (2) | トラックバック (1)

ガウス和に向けた準備(3) [ 数学 ]

今までの計算法をまとめると次のようになる。 $p$ は奇素数とし， $p-1=ef$ とする。1の原始 $p$ 乗根 $\zeta$ とmodulo $p$ での原始根 $g$ を一つ選んでおき， $f$ 項周期
$\eta_\nu=\sum_{j=0}^{f-1} \zeta^{g^{ej+\nu}} \qquad (\nu=0,1,2,\ldots, e-1)$
を考える。また，
$\eta^{(\lambda)}=\sum_{j=0}^{f-1} \zeta^{\lambda g^{ej}} =\zeta^{\lambda}+\cdots$
とおく。これは $\lambda$ が $p$ の倍数でないときは， $f$ 項周期の別の表現 (つまり $\zeta^{\lambda}$ を含む周期) となる。 $\lambda$ が $p$ の倍数のときは， $\zeta^p=1$ により，単に $\eta^{(\lambda)}=1+\cdots+1=f$ となる。

このとき， $\eta^{(\lambda)}$ と $\eta^{(\mu)}$ の積は次のようになる。 $\eta^{(\mu)}$ に含まれる項を
$\eta^{(\mu)}=\zeta^{\mu}+\zeta^{\mu_1}+\cdots+\zeta^{\mu_{f-1}}$
とすれば，
$\eta^{(\lambda)}\eta^{(\mu)}=\eta^{(\lambda+\mu)}+\eta^{(\lambda+\mu_1)}+\cdots+\eta^{(\lambda+\mu_{f-1})}$
となる。

投稿者 sukarabe : 12:12 | この記事の固定URI | コメント (0) | トラックバック (0)

2005年11月04日（金曜日）

ガウス和に向けた準備(2) [ 数学 ]

周期の積に計算例の続き。前と同じく $p=13$ , $e=3$ , $f=4$ の場合。原始根は $g=2$ にとっている。 4項周期も前と同じく
$\eta_0=\zeta^1+\zeta^8+\zeta^{12}+\zeta^5\\ \eta_1=\zeta^2+\zeta^3+\zeta^{11}+\zeta^{10}\\ \eta_2=\zeta^4+\zeta^6+\zeta^{9}+\zeta^7$
とし， $\eta_1\eta_2$ を計算してみると，前回と同様にして，
$\eta_1\eta_2\\ =\zeta^2(\zeta^4+\zeta^6+\zeta^{9}+\zeta^7)\\ +\cdots\\ +\cdots\\ +\cdots$
となる。ここで $\cdots$ の部分は省略したが，前回と同じく，サイクリックにずらして縦の列をまとめると周期になっている。これは一般的にも簡単に示される。第1列を足したものは， $\zeta^6$ を含む周期である。同様に，第2列は $\zeta^8$ を含む周期，第3列は $\zeta^{11}$ を含む周期，第4列は $\zeta^9$ を含む周期となる。

ここで，次のような記号を導入すると便利だ。 $\eta^{(\lambda)}$ により， $\zeta^{\lambda}$ を含む周期を表す。正確には，
$\eta^{(\lambda)}=\zeta^{\lambda}+\zeta^{\lambda g^e}+\zeta^{\lambda g^{2e}}+\cdots$
とする。従って，
$\eta^{(1)}=\eta^{(8)}=\eta^{(12)}=\eta^{(5)}=\eta_1$
などとなり，また $\lambda$ が $p$ の倍数のときは，
$\eta^{(0)}=1+1+\cdots+1=f=4$
などとなる。この記号を用いて上の計算を書くと，
$\eta_1\eta_2=\eta^{(6)}+\eta^{(8)}+\eta^{(11)}+\eta^{(9)}\\ =\eta_2+\eta_0+\eta_1+\eta_2\\ =\eta_0+\eta_1+2\eta_2$
となる。要は最初の分配法則の展開のみを考え，あとはそこで出てくる項を含む周期になるはずだから，とやればよいのだ。

投稿者 sukarabe : 23:51 | この記事の固定URI | コメント (0) | トラックバック (0)

2005年11月03日（木曜日）

ガウス和に向けた準備(1) [ 数学 ]

円周等分方程式がらみの計算は実際にやってみると，非常にきれいで楽しい。ただし，一般的に記述するには少々めんどうな部分もある。 $p=13$ に対する4項周期の計算を少しだけ。

原始根として $g=2$ をとる。すると $g^k$ ( $0\leq k\leq 11$ ) を列挙すると
$1,2,4,\quad 8,3,6,\quad 12,11,9,\quad 5,10,7$
となるから，3個の4項周期
$\eta_0=\zeta^1+\zeta^8+\zeta^{12}+\zeta^5\\ \eta_1=\zeta^2+\zeta^3+\zeta^{11}+\zeta^{10}\\ \eta_2=\zeta^4+\zeta^6+\zeta^{9}+\zeta^7$
ができる。一般論につながる見通しの良い計算のためには，この順番で並べることが大切。つまり， $\left(\mathbb{Z}/p\right)^{\times}$ の巡回群としての構造がポイントとなる。

例えば， $\eta_{0}^2$ の計算は次のようになる。分配法則を使って計算するのだが，その際，項の位置をサイクリックにずらすと見やすくなる。
$\eta_0\cdot\eta_0=\zeta^1(\zeta^1+\zeta^8+\zeta^{12}+\zeta^5)\\ \hspace{40}+\zeta^8(\zeta^8+\zeta^{12}+\zeta^5+\zeta^1)\\ \hspace{40}+\zeta^{12}(\zeta^{12}+\zeta^5+\zeta^1+\zeta^8)\\ \hspace{40}+\zeta^5(\zeta^5+\zeta^1+\zeta^8+\zeta^{12})\\ \hspace{30}=\zeta^{2}+\zeta^{9}+\zeta^{13}+\zeta^{6}\\ \hspace{40}+\zeta^{3}+\zeta^{7}+\zeta^{13}+\zeta^{9}\\ \hspace{40}+\zeta^{11}+\zeta^{4}+\zeta^{13}+\zeta^{7}\\ \hspace{40}+\zeta^{10}+\zeta^{6}+\zeta^{13}+\zeta^{4}$
こうして，縦の列ごとにまとめてみると，第1列の和は $\eta_1$ となっている。同様に，第2列は $\eta_2$ , 第3列は( $\zeta^{13}=1$ なので)4，第4列は $\eta_2$ である。よって，
$\eta_0\cdot\eta_0=4+\eta_1+2\eta_2$
となる。

同様にして， $\eta_i\eta_k$ を $\eta_0$ , $\eta_1$ , $\eta_2$ で表すことができる。

投稿者 sukarabe : 09:59 | この記事の固定URI | コメント (1) | トラックバック (0)

2005年11月01日（火曜日）

WeilによるKummer全集の序文 [ 数学 ]

Kummer全集は1975年にやっと出版されたとのこと。Weilが序文を書いている。その冒頭部分を引用。

The great number-theorists of the last century are a small and select group of men. ... Most of them were no sooner dead than the publication of their collected papers was undertaken and in due course brought to completion. To this there were two notable exceptions: Kummer and Eisenstein. Did one die too young and the other live too long? Were there other reasons for this neglect, more personal and idiosyncratic perhaps than scientific? Hilbert dominated German mathematics for many years after Kummer's death [in 1893]. More than half of his famous Zahlbericht (viz., parts IV and V) is little more than an account of Kummer's number-theoretical work, with inessential improvements; but his lack of sympathy for his predecessor's mathematical style, and more specifically for his brilliant use of p-adic analysis, shows clearly through many of the somewhat grudging references to Kummer in that volume.

要約すればこんな感じか？
「19世紀の偉大な数学者(数論に業績を残した)の多くは死後直ちに全集が企画・出版されたが，クンマーとアイゼンシュタインの全集は何故か出版されずじまいであった。科学とは関係のない個人的事情，イデオロギー的理由があったのだろうか？クンマーが1893年に亡くなったあと，ヒルベルトがドイツの数学界を長年に渡って支配してきた。ヒルベルトの有名な「数論報文」は内容においてはクンマーの業績に加えるものがほとんどないが，ヒルベルトには先駆者であるクンマーの数学上のスタイルと彼の素晴らしいp進解析に対する敬意が感じられない。それは「数論報文」の中でのクンマーへの言及がいかにも渋々であることによく現れている。」
英語苦手なので，誤読しているかもだが。

まあヒルベルトはデテキントのイデアルを基礎としたわけだし，クンマー流のうさんくさい(？)理想数なんか無視(笑)したいのかも知れなかった。当時は，Dedekind-Hilbert流のイデアルが支配的で，一方のKummer-Hensel-Hasse のp進解析の派閥(？)は傍流というか，まあそんな感じだったらしい。ヴェイユは歴史にも造詣が深いので，Eisenstein, Kronecker, Kummer あたりが埋もれてしまっているのが面白くないのだろう。実際，Eisensteinの楕円関数の理論なんて，一様収束とかの厳密性を別にすれば，ほとんどワイエルシュトラスの「ペー関数」と同じ事をずっと前にやっているのだが，何故か知られていない。アイゼンシュタインは早死にしたのが原因かも知れないが，クンマーは長生きしすぎたからか，とは冗談がきつい。

そうそう，本屋でヴェイユの「アイゼンシュタインとクロネッカーによる楕円関数」を見た。2500円。うちにある原書より安くて日本語になっているのが恨めしい(笑)。

投稿者 sukarabe : 16:44 | この記事の固定URI | コメント (0) | トラックバック (0)

ガウス和の端緒 [ 数学 ]

ガウスの和は，次の式で定義される。
$G=\sum_{a=1}^{p-1} \left(\frac{a}{p}\right)\zeta^a$
ここで， $p$ は素数， $\left(\frac{a}{p}\right)$ は平方剰余記号，そして $\zeta$ は1の原始 $p$ 乗根。もっと一般に拡張されたものもあるが，一番素朴な本来のガウス和がこれ。一番素朴な形ではあるが，これだけでは，この式がどこから出てきたのか分からない。数論の教科書には定義や性質は書いてあるものの，由来や動機付けがないことが多いのが不満の一つだ。

ガウスの「数論研究」を読むと，円周等分方程式の研究から自然に出てくることが分かる。簡単な例として， $p=7$ の場合(円周7等分)を考えてみる。この場合，原始根として3がとれるので，
$3^0=1,\quad 3^2=2,\quad 3^4=4$
の3つが平方剰余，残りの3,5,6が非剰余となる。そこで，1の原始7乗根 $\zeta$ のベキをこの2種類に分けて，周期
$\alpha=\zeta+\zeta^2+\zeta^4, \quad \beta=\zeta^3+\zeta^5+\zeta^6$
を作る。すると，簡単な計算で，
$\alpha+\beta=-1, \quad \alpha\beta=2$
となるので， $\alpha$ , $\beta$ は2次方程式 $x^2+x+2=0$ の根 $\frac{-1\pm\sqrt{7}i}{2}$ となる。よって，
$\alpha-\beta=\pm\sqrt{7}i$
となる。これが， $p=7$ の場合のガウス和に他ならない。つまり，
$G=\zeta+\zeta^2+\zeta^4-\zeta^3-\zeta^5-\zeta^6=\pm\sqrt{7}i$
である。一般の場合も同様にして $\sqrt{p}$ が出てくる。これはなかなか素敵な結果だ(^_^)。

さて，これを踏まえて最初の定義を見てみよう。なるほど納得できるではないか。良かった良かった。

投稿者 sukarabe : 12:13 | この記事の固定URI | コメント (0) | トラックバック (0)

2005年10月30日（日曜日）

Lemmermeyer氏の本，誤植多すぎ [ 数学 ]

相互法則について書かれたFranz Lemmermeyer氏の本 Reciprocity Laws:From Euler to Eisenstein を読んでいるのだが，誤植が多いのにはあきれた。おかしいなと気付いたのは，cyclotomic numbersの定義(p.101)がどう考えても間違っていることから。
$(r,s)=\sharp\{(a,a+1)\mid a\equiv g^{kn+r}, b\equiv g^{ln+s} \pmod{p}\text{ for some }k,l \}$
$g$ はmod $p$ での原始根であり，オーダー $n$ のcyclic numbersの定義なのだが， $b$ は明らかにおかしい。 $a+1$ の間違いだと思うが，念のためにと，検索してLemmermeyer氏のサイトをみつける。この本のページがあり，そこから正誤表がダウンロードできる。案の定なのだが，それよりも訂正が多いのには苦笑するしかない。

投稿者 sukarabe : 11:31 | この記事の固定URI | コメント (0) | トラックバック (0)

2005年10月28日（金曜日）

3次剰余とガウスの定理 [ 数学 ]

だいぶ前になるが，Silverman-Tateの本(楕円曲線上の有理点)を読んでいたら，ガウスの定理というものが書いてあった。ガウスの名前がつく定理はもちろん沢山あるわけだが，これは知らなかった。その定理はガウスの「数論研究」の第358節にあるという。

第358節は円周等分方程式の章，つまり，例の正17角形の作図が可能であることの証明が書いてある章にある。作図の可能性では2次方程式に還元するのだが，ガウスは3次方程式になる場合など，いろいろな例を調べている。3次の場合に面白い話があるとは知らなかった。うかつだなあ(苦笑)。改めて読んでみると，普通のガウスの和，つまり2次のガウスの和以外にも，3次のガウス和がすでに考察されていることが分かる。 3で割って1余る素数 $p$ つまり $p=3f+1$ の場合に， $f$ 項周期を考えることにより，次の命題が証明されている。

$p\equiv 1 \pmod{3}$ のとき， $4p$ は $4p=a^2+27b^2$ ( $a\equiv 1 \pmod{3}$ ) と一意的に表される。そして，有限体上での方程式
$x^3-y^3\equiv 1 \quad \pmod{p}$
の解の個数を $N$ とすれば，
$N=p+a-2$
となる。

ガウスはもちろん有限体での解の個数という言い方をしていないが，Silverman-Tateと読み比べると，そういうことだと分かる。ガウスの導き方は初等的だがトリッキーな式変形があり，ちょっとつらいなあと感じる箇所がある。その点Siverman-Tateの書き方はずいぶんと整理されていて読みやすい。ただ，Silverman-Tateの方は射影平面で考えているので，無限遠点での解が追加されている。そこだけ注意すれば翻訳は難しくない。

投稿者 sukarabe : 09:22 | この記事の固定URI | コメント (0) | トラックバック (0)

2005年10月22日（土曜日）

不味い数学の問題 [ 数学 ]

先週のことだが，ひさびさに不味いものを食った。といっても数学の問題だが。味覚と同様に問題の善し悪しは人により様々だが，こんなものが旨いと思う人が居るのかなあ？

見た目は整数の問題。自然数からなる集合Aに対してA'を次のように定める。奇数はそのまま，偶数は2で割る。例えば A={2,3,4,7,8,12} のときは A'={1,2,3,4,6,7} となる。問題は，二つの自然数からなる集合A, Bに対して (A∩B)'⊆A'∩B' となることを示せ，というもの。こんなの自明でしょ？

自明であることは一般化すれば，より明らかになる。一般化した命題は次のようになるだろう。写像 f:X→Y が与えられたとき，Xの部分集合A, Bに対して，f(A∩B)⊆f(A)∩f(B) であることを示せ。というわけで，整数とか偶数・奇数とかは本質と関係ないのであった。ああつまらない。もっとも「解けなかったら一般化せよ」というポリアの格言(？)が当てはまる例ではあったのだが。そう考えるとなかなか良い問題なのか？(苦笑)。

投稿者 sukarabe : 08:20 | この記事の固定URI | コメント (0) | トラックバック (0)

2005年10月19日（水曜日）

趣味の数学 [ 数学 ]

少し暇になったら18世紀から19世紀あたりの数学で気になるものを勉強というか鑑賞したいのだが，なかなかねえ。もっとも暇は自分で作るものという話もあった。

さしあったって数論と射影幾何(代数曲線)あたりが候補なのだが・・・。数論は以前ディリクレの講義録(デデキントが編集したもの)をノートを作りながら途中まで読んだ。2次体ではなくガウス直伝(？)の2次形式でやるもの。かなり読んだし面白かったのだが，種の理論あたりで挫折。というか，指標で定義する以外の定義はないだろうか。それが気に入らずにそれっきりなのだ。

射影幾何も気になりながらきちんと勉強したことがない。Semple-Kneeboneの教科書(イギリス流の古いスタイル)は直感的で読みやすいのだが，厳密にはどうなのか，と時々気になることもある。例えば例のポンスレーの定理(閉形定理)の証明は(2,2)対応でやってあるが，代数的対応の議論は何となく怪しい感じを受ける。現代的な理論，つまりスキームに基づく代数幾何を勉強すれば良いのだろうが，それができるなら苦労しないよ(苦笑)。

なんだかんだで思うにまかせないのだった。やれやれ，数学は難しいねえ。

投稿者 sukarabe : 12:08 | この記事の固定URI | コメント (4) | トラックバック (0)

2005年10月15日（土曜日）

リマソンの極方程式 [ 数学 ]

[備忘録として記録] リマソンの一般形(というか定義も)はよく知らないのだが，ここで考えるのは
$x=\cos\theta+\cos 2\theta, \quad y=\sin\theta+\sin 2\theta$
とパラメータ表示されるもの。多分，特殊な場合かな。

さて，某君の指摘で，極方程式で簡単に表せることを知った。和を積に直す公式を使い， $\frac{3}{2}\theta$ を改めて $\theta$ とおく。すると極方程式
$r=2\cos\frac{\theta}{3}$
が得られる。なるほど！

投稿者 sukarabe : 08:18 | この記事の固定URI | コメント (0) | トラックバック (0)

2005年10月08日（土曜日）

ストランド誌の難問コーナー [ 数学 ]

以前，ラマヌジャンの伝記「無限の天才」で見つけた面白い問題。210ページにある。何でもイギリスの大衆紙「ストランド」の1914年12月号の「難問コーナー」の載った問題らしい。ストランド・マガジンと言えばシャーロック・ホームズもこの雑誌じゃなかったっけ？

ともかく，その問題は次のようなもの。時節柄，ドイツ軍とか出てくるが，まあ，それはそれ。

「先日のことだが」とウィリアム・ロジャースは宿屋の暖炉に集まった村人たちに語りかけた。「ドイツ軍が焼き払ったベルギーのルヴェンのことで，ある旦那と話していたんだ。旦那が言うには，自分はその町を知っている。そこに友人が住んでいてよく厄介になっていたんだ，と。その友人の家は1番，2番，3番，・・・と家番号のついた大通りにあるんだが，驚いたことに，やつの家から右にある家の番地を足した数と，左にある家の番地を足した数が同じになるんだな。この通りには，50軒以上の家，といっても500軒以下だが，の家が並んでいる。この話を牧師さんに言うと，鉛筆をすらすらと走らせて，ベルギーの友人の番地をあてちまったんだ。はて，どうやったのね。」

さて読者はお分かりだろうか。

さて，友人から「君にお誂えの問題だよ」と言われたラマヌジャンの頭には直ちに一般解を与える一つの連分数が浮かんだという。「自然に浮かぶ」あたりがラマヌジャンの常人とは違うところだが，それはおいておいて，凡人なりに解いてみよう。

ラマヌジャンの頭の中はさすがに分からないが，この程度の問題なら何とか理解はできる。大通りに $n$ 軒の家があり，友人宅が $m$ 番地とすれば，
$1+2+3+\cdots+(m-1)=(m+1)+(m+2)+\cdots+n$
であるから，整理すると
$2m^2=n(n+1)$
となる。ここで， $n$ と $n+1$ には共通の素因数がないことに注意すれば， $n$ が偶数なら， $n+1$ , $\frac{n}{2}$ が共に平方数であり， $n$ が奇数ならば， $n$ , $\frac{n+1}{2}$ が共に平方数となる。この平方数を $x^2$ , $y^2$ とおけば，方程式
$x^2-2y^2=\pm1$
が得られる。これは所謂ペル方程式であり，その一般解は $\sqrt{2}$ の連分数展開から求められるのだった。ラマヌジャンの示した連分数はおそらく $\sqrt{2}$ のものではなく，直接 $\frac{n}{m}$ を与えるものなのだろうが，それは一体どうすれば求められるのか？

ともあれ，この問題は解けた。 $50\leq n\leq 500$ なる範囲では答えは一つに限る。それは
$1+\frac{1}{2+\frac{1}{2+\frac{1}{2}}} = \frac{17}{12}$
から出るもので， $x=17$ , $y=12$ , 従って， $n=288$ , $m=204$ となるのだった。

投稿者 sukarabe : 20:22 | この記事の固定URI | コメント (0) | トラックバック (0)

p進数 [ 数学 ]

p進数が数論で重要であることをずっと知らなかった。そもそも学部で数論の授業はなかったと思う。初等整数論は代数学の初歩(モジュールや群・環など)に含まれていたが，数論としての講義があった記憶がない。皆適当に自習していたようだった。門外漢としては，デデキント環とか付値論とかを通して何となく代数的数論のまわりをうろついていただけ。ヘンゼルが関数論におけるベキ級数のアナロジーとしてp進数を考えたらしいことぐらいは，おぼろげに知っていたが，そういうものもあるという程度で，主流はデデキントのイデアル論だと思っていた。

最近の数論の入門書をいろいろ見ると，p進数が知らないうちに主役(？)となっているので驚くのであった。ふーむ。

そういえばセールの「数論講義」でもp進体が解説してあったなあ。イデアルも代数体もなく，不思議な数論の本だと思っていたが，今になって思えば，あちこち合点がいくのであった(苦笑)。

本棚に Cassels の Local Fields という本がある。ずっと前に買ったのだが，未読のまま。最初のイントロを読んでみたが，これが意外に面白いことに初めて気付いた。付値の定義のあと，応用として von Staudt, Clausen の定理なるもののp進数による証明が載っている。この例が素晴らしいのだ。この先を読んでみようという気に十分なる。というか，付値論だけ延々とやられても退屈なのだが。

von Staudt, Clausenの定理というのは，ベルヌーイ数の分母を決定するもので，正確なステートメントは次の通り。「ベルヌーイ数 $B_n$ と $(n-1)$ を割り切る素数 $q$ に対する $\sum\frac{1}{q}$ の和
$W_n=B_n+\sum_{q}\frac{1}{q}$
は整数である。」証明はいろいろあるらしいのだが，ここで紹介されているのは， $p$ 進付値(による距離) $|W_n|_p$ を考えたとき，すべての素数 $p$ に対して，
$|W_n|_p \leq 1$
となるというもの。 $|W_n|_p \leq 1$ とは， $W_n$ の分母が $p$ を含まないということだから，それがすべての素数 $p$ で成り立つには整数しかないという論法。そして，これは孤立した結果ではなく，最近の研究の出発点でもあると書かれている。

最初にこんなものを見せられたのでは読まないわけには行かない(笑)。少し読んでみようかなと思う。できれば学部生の頃に，こういう具体例からp進数に馴染みたかったなあと思う。そうすれば，p進数体が奇異なものではなく，有理数体の完備化として実数体や複素数体と同等の地位を占めるものである，ということが理屈ではなく実感として感じ取ることができたのではないか，と思う。

投稿者 sukarabe : 15:12 | この記事の固定URI | コメント (0) | トラックバック (0)

2005年07月06日（水曜日）

微分積分学の基本定理 [ 数学 ]

微積の学習は，とかく計算技術に偏りやすい。意味を強調したいのだが，高校の教育がまずいせいか，一度染みついたものは，なかなか抜けないようだ。

どうしてこんなことを書いているのかというと，不定積分(原始関数)の計算で何故面積が求められるのか，という根本の所を理解していない学生があまりにも多いからだ。僕自身は，遠山啓「数学入門(上)(下)」とクーラント&ロビンズ「数学とは何か」で微積分を学んだので，幸いにもそのようなことはなかった。そんなことを考えながら，本棚から久し振りにクーラント&ロビンズを取り出してみた。

以下，449ページから引用。

ある種の教科書においては，名称の選び方がまずいため基本定理の際立った点が不明確になっている。多くの著者はまず導関数を導入し，次に $G' (x) = f (x)$ ならば $G (x)$ は $f (x)$ の不定積分であるという言い方をして，「不定積分」をただ導関数の逆と定義している。そこで彼等の方法によると，微分は直接に「積分」という言葉と結びついている。後になって面積あるいは和の極限としての「定積分」の概念が導入されるが，「積分」という言葉が今度は全く異なったものを意味するということは強調されない。このようにして理論の主要な事柄が裏口からこっそり持ち込まれ，学生の正しい理解に達しようとする努力が著しく妨げられる。 $G' (x) = f (x)$ であるような関数 $G (x)$ は「不定積分」ではなくて $f (x)$ の原始関数(primitive function)と呼んだ方がよい。そうすれば基本定理は単に次のようになる:
固定された下限と変化しうる上限を持つ $f (u)$ の積分 $F (x)$ は $f (x)$ の原始関数の一つである。 (以下省略)

投稿者 sukarabe : 00:19 | この記事の固定URI | コメント (1) | トラックバック (0)

2005年06月25日（土曜日）

大昔に買った本 [ 数学 ]

捜し物があって本棚をローラーシフトしていたら，昔々，高校生の時に買った「代数曲線論入門」(河田敬義著，至文堂)が出てきた。たしか自分で買った数学書としては2冊目のはず(一冊目は数論の入門書)。高校2年生の夏休み，家族旅行の途中，東京に寄ったときだった。ホテルが神保町だったので，父と一緒に本屋巡りをしたのだった。田舎の本屋しか知らなかったので，書泉グランデを初めとして圧倒された記憶がある(笑)。数学の本も選り取り見取りだ！何故，この本を選んだのか分からないのだが，無謀であったことだけは間違いない(苦笑)。

日本の数学の本は総じて難しい。入門と銘打ってあっても，本当の入門書は希だ。まあ専門書から比べればということなのだが。この本も237ページの小冊子にもかかわらず，内容は豊富だ。目次をざっと拾ってみよう・・・。

全体は3部に分かれている。第I部は平面代数曲線論。第1章平面代数曲線，第2章有理変換，第3章素点，第4章単純点と重複点，第5章形式的ベキ級数，第6章曲線の交差，第7章プリュッカーの公式，となっている。このような古典的な代数曲線の話は日本語では案外ない。英語だと Walkerの Algebraic Curves とかあるけど。そう考えるとなかなか良い本かな？今なら読めそうだし(笑)。

さて，第II部と第III部は紙数の関係で駆け足の解説になっている。第II部は，代数関数体の代数的理論。第8章リーマン・ロッホの定理。むむむ・・・なんとアデールを用いた証明。岩澤先生の「代数関数論」と同じですね(笑)。はあ，そうだったのか。今になって初めて知るこの事実。気を取り直して先に進もう。第9章代数関数体の微分，第10章リーマン・ロッホの定理の応用。第III部はリーマン面の理論，ということだが，もう紙数がないので，ホントに駆け足。第11章代数関数体の解析的理論。内容は，リーマン面，リーマン面の位相幾何，第1種アーベル微分，アーベルの定理，ヤコビの逆問題，楕円曲線，以上。

別の本で勉強してから読むと，良くできたレジュメとして重宝するかも(笑)。

投稿者 sukarabe : 08:11 | この記事の固定URI | コメント (0) | トラックバック (0)

2005年06月15日（水曜日）

レムニスケート5等分の計算 [ 数学 ]

ガウスが円周の等分に引き続いて，レムニスケートの等分を試み，それがきっかけで楕円関数の一般理論を発見したことは良く知られている。また，ガウスが「数論研究」で円周等分と同様のことが，積分 $\int \frac{dx}{\sqrt{1 - x^{4}}}$ に関係する関数(つまりレムニスケート関数)にも適用できると，さりげなく示唆したことが刺激となり，アーベルによる楕円関数の発見および等分理論，さらにはアーベル方程式につながったことも，良く知られている。

そうなんだけど，歴史の本や通俗解説書には，お話しか書いてない。一方，数学書の方は，入門書であっても，いきなり楕円曲線や虚数乗法の一般論になってしまい，それらがどのような経緯で発展してきたのか，具体的にはなかなか書いてないように思う。

ささやかではあるが，そんな状況を補うような本を見つけた。

見つけたといっても自分の本棚で。買ってはみたが，ちゃんと読んでなかったことが，ばればれだね(苦笑)。

AMSでロシアの数学書から選んで翻訳しているシリーズがあるのだが，その中の一冊。Prasolov, Solovyev の共著で，"Elliptic Functions and Elliptic Integrals" (楕円関数と楕円積分)というタイトル。第5章が「レムニスケートの分割に関するアーベルの定理」という題で，ガウスによる円周17等分(正17角形の作図)から始まって，具体的な計算も含めて，理論がどのように進展したのか分かるように解説してあって楽しい。もちろんすべての計算が self-contained で書いてあるわけではなく，ギャップもあるのだが，それらは普通の教科書で補うことができる。

レムニスケートの話は，弧長の積分表示とその逆関数としてのレムニスケート関数 $f (x)$ の導入に始まり，加法定理，倍角公式などと続く。三角関数とパラレルになっていることが分かる。レムニスケートを5等分するには，方程式 $f (5 x) = 0$ を解くのだが，素数5がガウスの複素整数の範囲で， $5 = (2 + i) (2 - i)$ と分解されることに基づき， $(2 + i)$ 倍角公式と $(2 - i)$ 倍角公式を作って，25次方程式をより低次の方程式に帰着させ，結局は平方根のみで解けることが示されている。ここまで書いてある本はなかなかないのでは？というか，普通は自分でやれ，と言われるかも(苦笑)。

このような計算が可能であるのは，レムニスケート関数の場合 $f (ix) = i f (x)$ という等式が成り立つからだ。これがある故に $(2 + i)$ 倍角の公式などを作ることができる。これこそが「虚数乗法」の最初の例だったりするのだが，その意味では，この計算そのものが(けっこう面倒なんだけど・・・)もっと知られて良いのになあ，と思う。

さて易しい話はここまでで(笑)，このあと一般論に移る。レムニスケートの等分方程式が代数的に可解であることの証明。アイゼンシュタインの証明と，現代風のローゼンの証明の概略が書いてあるが，現代風のは，やはりかなり抽象的だなあ・・・と。

投稿者 sukarabe : 08:08 | この記事の固定URI | コメント (1) | トラックバック (0)

2005年03月10日（木曜日）

いやはや [ 数学 ]

[この記事の数式は、MathMLで記述されています。MathMLをレンダリングできないIEで正しく表示するためには、MathPlayer(無料です)をインストールして下さい。]

若い同僚で Mi君というのが居るのだが、頭が良すぎるので困ってしまう。今日も彼の原稿を見ていて、参ってしまった。

問題は、 $0$ 以上の実数 $s$ , $t$ が $s^{2} + t^{2} = 1$ を満たすとき、 $x^{4} - 2 (s + t) x^{2} + (s - t)^{2} = 0$ という複2次の方程式の実数解の取りうる範囲を求めよ、というもの。さて、Mi君のコメントは次の通り。 $x^{2} = u$ とおけば、この方程式は、 $s^{2} + t^{2} + u^{2} = 2 (st + su + tu)$ と書け、 $s$ , $t$ , $u$ について対称な形となる。従って、 $s + t + u = 2 k$ とおけば、 $s$ , $t$ , $u$ は、3次方程式 $z (z - k)^{2} = a$ の3解となる、というもの。

なるほどねえ・・・。よくこんなことに気付くよなあ。これが才能というものだろうか。ああ、僕の才能はどこに消えてしまったんだろう(苦笑)。

投稿者 sukarabe : 21:11 | この記事の固定URI | コメント (1) | トラックバック (0)

2005年02月27日（日曜日）

もう歳だよなあ・・・ [ 数学 ]

少し前から、凡ミスの頻度が激増していて、墓場が近いことを予感させていて、けっこう憂鬱なのだが、またもやってしまった。こんな事を書くのは恥以外の何物でもないが・・・。

a²-a が 10000で割り切れるような、3 以上 9999 以下の奇数をすべて求めよ、という問題。a と a-1 が互いに素なので、10000 を素因数分解すれば、a が 5⁴=625 の倍数で、a-1 が 2⁴=16 の倍数であることが必要十分であることが分かる。これから、a=625x, a-1=16y とおける。a を消去すれば、いわゆる不定方程式 625x-16y=1 ができる。625=16x39+1 に気付けば、これを解くことは簡単で、その結果、a の一般形である
a=625(16t+1) (tは整数)
を得るのだが、さあ、お立ち会い、ここで恥ずかしいミスというか書き損じだ。

3≦a≦9999 となるのは、t=1 の場合に限られるので、求める aは a=625 のみである。

いや、こんなしょうもないミスはしょちゅうなんで、別にいいんだけどさ・・・。でも、誓ってもいいが、10年前だったら、絶対にこんなことはしないからね！

あ～でもいらいらする！(苦笑)。

投稿者 sukarabe : 14:44 | この記事の固定URI | コメント (0) | トラックバック (0)

2005年02月16日（水曜日）

itex2MMLのテスト [ MovableType, TeX, コンピュータ＆インターネット, 数学 ]

とりあえずテストをしてみる。ソースコードはこれ。

\frac{1}{2}+\frac{1}{3}+\frac{1}{7}+\frac{1}{42}=1

それで出力結果は，次の通り。 $\frac{1}{2} + \frac{1}{3} + \frac{1}{7} + \frac{1}{42} = 1$

WindowsのIEで見るには，MathPlayerをインストールする。Firefoxならデフォルトで見れるが，数式フォントが無いと表示がおかしくなるので，Mozilla/MathML/FontsあるいはMITが配布している数式フォントを一式ダウンロードしてインストールしたほうが良いのかな？

投稿者 sukarabe : 17:19 | この記事の固定URI | コメント (0) | トラックバック (0)

itex2MML Plugin for MovableTypeを導入する [ MovableType, TeX, コンピュータ＆インターネット, 数学 ]

itex2MMLはLaTeX風に書いた数式表現をMathMLに変換してくれるプログラムである。現時点ではJacques Distlerという方が開発・保守されているようだ（最初は別の人だったみたいだが）。そして，このitex2MMLをMovableTypeで使うためのText Filter Pluginもある。これを導入してみた。

itex2MML Plugin for MovableTypeの導入手順

まずJacques DistlerさんのWebLogにあるitex2MML Pluginのページに行く。Source distribution とあるところをクリックして一式をダウンロードする。解凍すると，itex2MMLのソース・コードとMacOSX用にコンパイルしたバイナリー，それからMovableTypeで使うための itex2mml.pl がある。自分でコンパイルできる人はそうすればよいが，そうでない場合（つまり僕の場合）はバイナリーをどこかで調達する必要がある。

ローカルで使うのではなく，サーバー上で使いたいわけだから，サーバーのOSに合わせる。ここのようにLINUXであれば，James GrahamさんのところにLinux/x86用のバイナリーがあるので，そこからダウンロードさせてもらう。それから，自分のサイトのサーバー上でのフルパスを調べておく。ロリポップだと，
/home/sites/lolipop.jp/users/....../web/
のようになっていると思う。以上で準備はOKだ。

準備ができたら作業に入る。

itex2MMLの本体，つまり実行ファイルを適当な場所にアップロードする。僕の場合は，自分のサイトのホーム直下にbinというフォルダーを作ってそこに入れた。そして，属性を755などの実行可能なものに変更する。
MovableType用のプラグインであるitex2MML.plをテキスト・エディターで開く。ここで，/usr/local/bin/itex2MMLと書かれているところが2カ所ある。これを自分がアップロードした場所に変更する。僕の場合だと，
/home/sites/lolipop.jp/users/......../web/bin/itex2MML ということになる。
編集が終わったitex2MML.plをMovableTypeのプラグイン・フォルダーにアップロードする。
MovableTypeのエントリー編集画面で，テキスト・フォーマットの選択肢に，itex to MathML と itex to MathML with parbreaks の２つが増えているはず。

以上で作業は終了，と言いたいのだが，MozillaがMathMLを表示するには，HTMLではなくXMLにしておかねばならないらしい。ここいらになると良く分かってないので困るのだが，付属の解説やWeb上の説明を読むと，ページの情報みたいな所に，Content-Typeはapplication/xhtml+xml だよ，ということを書いておけということらしい。

良くは分からないなりに，XHTML1.1+MathML2.0の文書という宣言をすることにした。とりあえずトップページだけだが。そして，Content-Typeをtext/htmlからapplication/xhtml+xmlに変更する。W3Cに行ってチェックすると，いきなりNOT VALIDと表示されてしまう。対処療法で，駄目と言われたところをコメントアウトする。（検索のフォームが文法違反と言われたので，現在削除中です。）とりあえずなんとかValid XHTML1.1+MathML2.0をクリアーする。

さあ，実験だ，ということで，簡単な数式を書く。

 \frac{1}{2}+\frac{1}{3}+\frac{1}{7}+\frac{1}{42}=1

というLaTeXコードでテストしてみる。これがMathMLに変換されると，

\frac{1}{2} + \frac{1}{3} + \frac{1}{7} + \frac{1}{42} = 1

と表示されるはず。これが全然駄目。いろいろ試みるうちに，ファイルの拡張子を.htmlから.xhtmlに変更すれば，ちゃんとレンダリングされることを発見した。しかしなあ・・・.htmlのままでもMathMLが表示されているページはいくつもあるのになあ・・・。このページも.htmlのままだから，多分表示されないだろう。あー，疑問だらけだ！

さらに具合の悪いことに気づく。出力をindex.htmlからindex.xhtmlに変更し，古いindex.htmlを削除したところ，フォルダーのURLでアクセスした場合に，ファイルが存在しません，というエラーメッセージが出てしまう。え～index.phpとかindex.cgiはOKなのになあ・・・。ということで，これも見よう見まねで，.htaccessファイルを書く羽目になる。
DirectoryIndex index.xhtml と設定する。index.htmlにアクセスされたときのために，リダイレクトもした方が良いだろうか。うーむ。

これだけ頑張ったのだが，十分とは言えないなあ。もう少し勉強しないと。それに，Mozilla系はちゃんとMathMLをレンダリングするが，Internet Explorerが全然サポートできてないので，大多数の人はそのままでは数式が見れない。WindowsであればDesign Science社からInternet Explorer用のMathMLレンダリング・プラグイン MathPlayer が無償で配布されているから，それをインストールすれば見られるんだけどね。

追記

結局，ブロッグのトップのディレクトリーで .htacess に次のように書き加えることで一応の解決を見た。これは，Jacques Distlerさんの解説にあったものをほとんどコピーしたものだが，一カ所だけ変更してある。それは，index.shtml とあったところを index.html と変えたところ。だって，shtmlファイルはうちにはないから。それから RewriteBase のところは，ドメイン名というかサイトの直下をルートと考えたときのパスを書くと良いみたい。うちは直下に mt フォルダーを作って，そこにブロッグのトップがあるので，そのパスを書いた。

RewriteEngine On
RewriteBase /mt/
RewriteRule ^＄ index.html
RewriteCond  %{HTTP_USER_AGENT} Gecko|W3C.*Validator|MSIE.*MathPlayer
RewriteRule \.html＄|\.shtml＄   - [T=application/xhtml+xml]
RewriteCond  %{HTTP_USER_AGENT} Chimera|Camino|KHTML
RewriteRule \.html＄|\.shtml＄   - [T=text/html]
RewriteCond  %{HTTP_USER_AGENT} Camino.*MathML-Enabled
RewriteRule \.html＄|\.shtml   - [T=application/xhtml+xml]

ちなみにドル記号は itex2MML を使うときは数式の始まりと認識されてしまうので，全角文字の＄で表記した。使うときは半角に。というかドル記号の実体参照ってないのかな？

投稿者 sukarabe : 15:50 | この記事の固定URI | コメント (2) | トラックバック (0)

2005年01月29日（土曜日）

いまさらルベーグ積分？ [ 数学 ]

正直言ってルベーグ積分はきちんと理解していない。リーマン積分よりも一般的で，積分と極限を交換してよいとか，便利なものだ，というくらいの認識。大体，基礎となる測度論にあまり興味が持てなかった。可算加法性がどうして重要なのかとかピンとこないことが多かった。

前にちょっとだけ書いたことだが，エミール・ボレルの「一般集合論」という啓蒙書というか入門書を読んでいるのだが，目からうろこではないが，なるほど，と納得してしまった。なんかちょっと嬉しいな！

大体，ルベーグ積分の教科書では，ボレル集合とか出てきるが，ボレルの名前はそこで終わりで一体何なんだろう，と思っていたのだった。ボレルの本を読むと，ルベーグに先駆けて重要な仕事をしていたことが分かる。

ボレルの本は専門書ではなく，大衆向けの啓蒙書という感じなので，具体的で非常に分かりやすい。線分の長さという概念を一般の集合（この場合は数直線，つまり実数全体の部分集合）にどう拡張するか，ということから始まって，まずカミーユ・ジョルダンによる測度の定義を述べる。その定義では，たとえば０と１の間にある有理数の全体は，外測度１，内測度０で，測度が定まらない。一方，０と１の間にある無理数全体についても同様の結果となる。

さてボレルは言う。有理数は無理数にくらべれば，限りなくまばらであるのだから，有理数全体と無理数全体の測度が等しいというのは，まさしく逆説的だ，と。そして，このことを解決するために，ボレルは新しい測度の定義を考えたのだと言う。後になり，ルベーグがボレルの定義に「Ｂ測度」という名を与えたのだそうだ。

０と１の間にある有理数は無理数よりもまばらである。カントールが示したように可算無限個（可付番）でしかない。そこで，それらを一列に並べる。最初の有理数を含む長さε/2の区間を考える。次に２番目の有理数を含む長さε/4の区間を考える。以下同様にして，区間の幅が公比1/2の等比数列となるようにする。０と１の間にある有理数の全体をＥで表すと，Ｅは上で作った区間の合併に含まれるが，この区間たちの長さを全部足しても，εにしかならない。つまり，集合Ｅの測度はεよりも小さいことが結論される。εは任意の正の値をとれるので，Ｅの測度は０でないとおかしいことになる。

こんな感じなのだ。もちろん今の話には，これから作ろうとしている測度の公理が暗黙裡に入ってはいるが，有理数が可付番個しかないということから測度が０でなければならないことが，きわめて自然に説明されている。ここで基礎となるのは可付番個の区間について長さの和をとってよいということだ。つまり可算加法性の重要性がはっきりする。

ボレルの説明は，このような初等的な例から始まって行くのだが，無限個の区間を扱う際の危険性とそれを避けるための基本定理が次に書いてある。その基本定理というのが，何とハイネ・ボレルの定理なのである。つまり今の言葉で言えば，閉区間がコンパクトであるという内容。脚注が付いていて，この定理がボレルの学位論文で初めて述べられ，かつ証明されたということが述べてある。

こうやって読んでいくと，高々可付番個しかない集合は測度０であるべきだ，という事，それから，集合を無限個の区間で覆っている状態から，（無限個のまま処理すると非常識なことも起こりうるということから）有限個でのカバーにもっていきたい，という事，ボレルの名前が付いている２つの事柄が密接に関係していたことが分かる。コンパクトの概念が測度論がらみで出てきたとは知らなかったなあ。

なんとなく心理的障壁を越えた気がしてとても嬉しい。もっとも測度論をまじめに勉強しようとは思わないんだけど（笑）。

投稿者 sukarabe : 23:37 | この記事の固定URI | コメント (1) | トラックバック (0)

2005年01月18日（火曜日）

初心者相手に1次変換 [ 数学 ]

どちらかというと仕事関係で日記を付けたことがない。とりたてて記録したいことがないのかもしれない。大体カテゴリーに仕事という項目を作ってなかった（笑）。ということで，あまり楽しくない記録をしておくか・・・。

まったくの初心者相手に1次変換を教える，という内容なのだが，これで困っている。あてがわれた教材はあるのだが，これが素晴らしすぎる（苦笑）。こんな感じで始まるのだった。

まず，唐突ですが，定義を先に書いてしまいます。平面ベクトルの全体から平面ベクトルの全体への写像 f が，さらに次の性質
f(x+y)=f(x)+f(y)
f(ax)=af(x)
をみたすとき，f を線形写像（一次変換）といいます。

数学科ならこれでも良いのかもしれないが，ちょっとこれじゃあ，あんまりだと，さすがに思った。相手は写像の概念すら，きちんとはないのに。おまけに，例題での1次変換の与え方が，基底の像を指定する形なのだ！つまり，こんな感じ。

平面上の1次独立な2つのベクトル a₁, a₂ に対して，
f(a₁)=a₁+2a₂, f(a₂)=-2a₁+a₂
となる線形写像 f がある。

おいおい，である。ゲームのルールを与えて後は規則に従っていけば数学が理解できるとでも言うのだろうか。一世を風靡した（？） general abstract nonsense ではないが，21世紀にもなろうとしているのに，このブルバキの不肖の末裔め！という感じだ。

ということで，次のような感じでやったみた。考えてみると，1次変換の授業というのは，一回もやったことがなかった（笑）。おい，大丈夫か？

関数の拡張というか，点を点に対応させるものとして，写像というものを定義する。具体例として，x軸に関する対称移動，原点のまわりの90度回転などを挙げる。
平面上での1次変換を（もちろん座標で）定義する。先に挙げた例が1次変換の特別な場合であることを説明。
座標で導入した1次変換の行列表示の説明。行列と縦ベクトルの積をここで定義する。
ここが面倒なところだが，1次変換の合成をやってみる。それと対応する形で行列の積を定義する。
ここらで簡単な練習問題を出す。一つは行列の積を計算すること。これは全員できた。のみこみは速いようだね。よかった，よかった。もう一つは，x |---> (a・x)a という1次変換の行列表示を求めよ，というもの。ここで，泥縄ではあるが，点と位置ベクトルを同一視することを説明（苦笑）。いやあ，準備悪いんで。2番目の問題は案外と難しいみたいだった。でも少しヒントを出すとOK。
恒等変換と単位行列の説明。それから，逆変換と逆行列。ついでに行列式 det(A) の定義も。
逆行列を使った簡単な例題。行列 A で定まる1次変換による正方形 0≦x≦1, 0≦y≦1 の像を求めること。補足として，線形性を利用した，つまりベクトル的に処理した解説もする。像が平行四辺形になることを理解するには，こっちの方が良い。
ここに至ってようやく線形性の説明。ようするに行列の計算では分配法則が成り立つということ。あ，しまった，分配法則の説明をやってなかった（笑）。まあ，しかし，この辺りは大丈夫みたいだった。

ここで時間が来てしまったので，今回はここまで。もう少し時間があれば，線形性を利用した簡単な例題をやりたかったのだが。例えば，一般の平行四辺形が1次変換で平行四辺形に写ることの証明など。まあ，次回にということで。

以上，昨日の授業の記録。

投稿者 sukarabe : 08:13 | この記事の固定URI | コメント (0) | トラックバック (0)

2005年01月15日（土曜日）

シュプリンガー東京から続々と数学の本が・・・ [ 数学 ]

何の気なしにシュプリンガー東京のサイトを見に行ったら，なんとワイル(Hermann Weyl)の The Classical Groups の翻訳が出版されているようだ。シュプリンガーも頑張っているというか，よく出すよねえ（笑）。というか蟹江さんという人，よくこんなに何冊も翻訳できるよなあ。

そう言えばこの本は岩堀先生が授業中によく薦めていたっけ。難しいと敬遠する人が多いけどとっても面白いからって。そう言われてもおいそれと手が出ないのが実情であった（苦笑）。翻訳されたといっても内容が易しくなるわけじゃないしね。もっともワイルの文章はいささか衒学的というか格調が高すぎて難しいということもあったから日本語だと敷居が低くなるだろうか。さてさて，いまさら読むか（読めるか）どうかは置いておいて（笑），本棚を飾るのに買ってみる？

ついでにサイトのあちこちを見てみると，驚いたことに最近出版された邦訳のリストに，ハーツホーン (Hartshorn) の Algebraic Geometry や，ザイフェルト，トレルファルの Lehrbuch der Topologie がある。ハーツホーンはともかく，ザイフェルトの教科書が学生時代に訳されていたらなあ，と思う。

ありゃ～，ハーディ，リトルウッド，ポリアの「不等式」まで邦訳が出ている・・・。し，知らなかったです（汗）。いやはや，シュプリンガー東京，恐るべしだな。

投稿者 sukarabe : 01:10 | この記事の固定URI | コメント (0) | トラックバック (0)

2005年01月11日（火曜日）

ある確率の問題 [ 数学 ]

本棚の整理をしていたら「確率問題ゼミ」（シュプリンガー・フェアラーク東京）が出てきた。この本で知った面白い問題を紹介しよう。

翻訳なので多分そういうテレビ番組がアメリカあたりであるのだろうと思うが，次のような設定。視聴者参加型のテレビ番組（クイズ番組だろうか）で勝ち抜いた人（Aさんとしよう）が，いよいよ賞品の車（日本だとパジェロとか，あ，三菱没落前ならね）をもらえるかどうか，という最終局面。でも簡単にはくれない。ドアが3つ用意されていて，そのうちの一つを選ばなくてはならない。一つのドアの後ろだけにパジェロがあり，他のドアの後ろにはヤギが居る（なんでヤギなんだろう，でもそう書いてあるんだもの）。

さて，迷いに迷った末に，Aさんは一つのドアを選ぶ。すると意地悪（？）な司会者が更に迷わせる質問をするのだった・・・。

さて司会者はどのドアの後ろにパジェロがあるかを知っている。そこで彼は一つのドア（もちろんAさんが選んでないもの）を開けてみせる。するとヤギが居る。司会者はAさんに言う。「Aさん，どうしますか。このまま選んだドアを開けますか？それとももうひとつのドアに変えますか？今なら変えてもいいですよ。これが最後です（ファイナルアンサーってことかね，笑）。どうします？」

さてここで問題です。Aさんはドアを変えた方が得なのでしょうか。それとも最初に選んだままにした方がいいのでしょうか。それともどちらでも同じなのでしょうか。答えは意外かもしれません。

投稿者 sukarabe : 20:44 | この記事の固定URI | コメント (5) | トラックバック (0)

2005年01月08日（土曜日）

基礎は大切か [ 数学 ]

昨日，会議中だか食事中だか忘れたが，雑談しているときにNi氏が次のようなことを言っていた。大阪の某S氏が言うには，e=2.718281... の定義だとかいろんな関係式が同値であることを証明させたりすることは必要なのか，そんなことをしても問題を解く力はつかないのではないか，と。はあ・・・そ，そうですか。そうかも知れませんね（苦笑）。

10年前に同じ事を言われたらムキになって反論したかもしれないな。どうなんでしょうか。

mimeTeXのテストも兼ねて数式を書いてみる。e というのは，
$eの定義式$
で定義される定数（Landauの言い方を真似れば，宇宙定数（笑））のこと。この定義と例えば
$eの定義（その２）$
が同値であることを示すのは易しくない。しかもそれができたら数学の力がつくかと言われるとたしかにそうかもしれないと思う。S氏の趣旨はおそらく，こういう基礎に関する事柄をやるよりも，もっと実践的な応用問題を解かせる方が良いのではないか，ということだと思う。

しかし，そんなことを言われたら，じゃあどんな問題を解けば数学の力がつくのだろうか，と思ってしまう。他人のことは分からないので自分の経験で言えば，高校生のときは（同級生たちに比べれば）あまり問題を解いてない気がする。たまにおもしろそうな問題のときは頑張って解いたと思うが，どちらかというと問題を解こうという元気はなかった。受験勉強はそれなりにしたと思うが，参考書の例題をながめて，ちょっと考えたらすぐ下の答えを読んで（笑），なるほどね，てな感じだった。

さて上の2つの式が同値であるという問題だが・・・困ったことに高校生のときにおもしろそうに感じる問題というのがこういう種類の問題だったのだ（笑）。だって不思議だもん！あはは。

Ni氏に限らず数学科の普通の感覚だと，こういう基礎の大切さを疑問に思うことの方が不思議で，え？なんでそんなこと聞くの？と思う方が多いかもしれない。もちろん，基礎をすべて理解して使っているとは限らないが。僕にしても分かってないことの方が多いくらいだ。ええと・・・ルベーグ積分（苦笑），スペクトル系列，CW複体，等々。気にはなっているんだけど。ルベーグ積分については最近，溝畑先生の本とボレルの本を読んでいて少しだけだけど，ああそういうことなのか，と分かってきたつもり。スペクトル系列は全然だめ。ヴェイユによるド・ラムの定理の証明で2重複体を利用するのがあるが，あれでいっぱいいっぱいだ。CW複体に至っては定義の意味が分かりませ～ん！包体複体(cell complex)とどう違うんでしょうか・・・。

話を戻すが，思うに，力をつけるには数学をやればよいだけであって，どの問題をとかいうのはあまり考えなくていいのではないのだろうか。食事に例えるのも変ではあるが，大切なことは，まず食べることだ。いちいち栄養があるかとか考えるだろうか。もちろん偏食は薦められないけどね。

投稿者 sukarabe : 12:11 | この記事の固定URI | コメント (7) | トラックバック (0)

2004年12月10日（金曜日）

正18角形の問題 [ 数学 ]

偶然みつけたBlogになつかしの問題が載っていた。

技術系サラリーマンの交差点: ５年考えて解けなかった問題

この記事が書かれたのはもう4ヶ月も前で，今頃トラックバックしているのは，なかなかに間抜けなのだった。ただ，大いに盛り上がっているコメントなどを一通り読んだのだが，この問題が正18角形の対角線を引くことにより作られているということがどこにも書かれてなかったように思う。見落としていたかもしれないが。

なつかしの問題と言ったが，この問題を解いたのは，昔々高校三年のときであった。誰に出されたのか，あるいは何かの本にあったのか，全然覚えてないのだが，解いたことと，三角関数を使ったこと，とくに三倍角の公式を利用したことだけは覚えている。できれば初等幾何でエレガントに解きたいものであるが，その方面の才能には恵まれていないのでやむを得ない（苦笑）。あ，もしかしたら，数学セミナーのエレガントな解答を求むで見たのかもしれない・・・。うーん，その可能性が高いような気がするなあ。

いずれにしても，個人的には，解答よりも，むしろいったいどうすればこんな問題を思いつけるのか？という興味の方が強い。その意味では，正18角形（頂角20度の二等辺三角形が18個できる）の対角線を引くとこの図ができるということを知ったときの驚きの方が，エレガントな解答よりもずっと強かった。

そう言えば少し前に買った初等幾何の本（CoxeterとGreitzerの共著 Geometry Revisited）にもこの問題が載っていた。けっこう有名なのかもしれない。

投稿者 sukarabe : 00:54 | この記事の固定URI | コメント (2) | トラックバック (0)

2004年11月16日（火曜日）

p=x²+y² [ 数学 ]

先日の「博士が愛した数式」がらみなのだが，p=x²+y²となる奇素数の必要十分条件が p≡1(mod 4) であることの簡単な証明を本屋で見つけた。というか，多分有名なんだろうし，本質的には既存の証明と変わりないとは思うが。

旭屋書店で数学書コーナーによってみたら，月刊誌「数学セミナー」がおいてあった。たしか以前は雑誌コーナーの方だったと思う。ひさしぶりにページをめくると，有名なんだけど案外証明をしらないもの（？）特集をやっていて，その中に平方数の和で書ける素数の話があったのだった。

ガウス整数（a+biの形の整数。ここでa, bは整数で，i は虚数単位）の枠内で考えると，この問題はガウス整数の素数を決定せよという，きわめて基本的な問題になる。「数学セミナー」に載っていた証明は，これとは違うが，有限体での「虚数単位」的なものを考えるという点では，アナロジーとして面白いと思った。

よくよく考えてみると実はどこかで読んだ証明と同じだったりするのだが，ちょっとした表現の違いや，立脚点の違いで，そうか，そうだったのか，と感じることは時々ある。今回もそんな感じだ。立ち読みしただけなので，細部を詳しくは覚えていないが，大体次のような道筋だったと思う。というか，部屋割り論法の所のアイディアだけしかちゃんとは覚えておらず，あとはこうすればできるかなあ，と適当に作ったので，もしかしたら少し違っているかも知れない。また立ち読みしにいくか（苦笑）。

pを4で割って1余る素数とすると，mod p で i²≡ -1 となる「虚数単位」的な整数 i が存在する。そこで，x+yi の形の整数を何個か作って，その余りを考える。ディリクレの部屋割り論法を使えば，余り0が必ずあることが示される。つまり，x+yi の形でpの倍数となる整数が存在することが言える。ここで，i²≡ -1 を利用すれば，
x²+y²≡(x+yi)(x-yi)≡0 (mod p)
となる。つまり，x²+y² はpの倍数となる。さて，最初の部分ではx, yを0とpの平行根の間にとっておくのである。すると，x²+y² は0と2pの間ということになり，pの倍数はp自身のみとなる。言い換えれば，めでたく，p=x²+y² と書けるということだ。うーん，美しい証明だ。ちょっと感動してしまった（笑）。

投稿者 sukarabe : 23:22 | この記事の固定URI | コメント (1) | トラックバック (0)

2004年11月13日（土曜日）

博士の愛した数式 [ 数学 ]

昨日，西武リブロにぶらっと寄ったら，入り口近くの平積みのところに「博士の愛した数式」という小説があった。帯に，本屋の店員が選んだうんぬんとあったのと，タイトルに惹かれてちょっとだけ立ち読みしてみた。まず最初のページ，次に最後のページというたちの悪い読み方（笑）。その他もパラパラと見たが，数学の部分は小学生でも理解できるもので，まあ小道具として使われているだけで，メインは「博士」と「私」，そして私の息子である「ルート」のほのぼのとした人間関係ということなのだろう。そうでなくては，こんなに人気があるはずはない。

WEB本の雑誌/書評・2003年の課題図書/博士の愛した数式（新潮社，小川洋子）

ということで，面白いとは思ったものの，買うところまでは行かなかったのだが，最終ページに書いてある内容は，なかなかの奥深い定理なのだった。

それは，例の，素数の形状に関するものだ。2以外の素数（それはすべて奇数なのだが）は4で割ったときに1余るものと，3余るものに分けられる。

4で割ったときに1余る素数とは，具体的に言えば，
5，13，17，29，37，etc.
である。これらは，すべて平方数の和として表すことができる。
5=1²+2²
13=2²+3²
17=1²+4²
29=2²+5²
37=1²+6²
こんな調子だ。
他方，4で割ったときに3余る素数
3，7，11，19，23，31，etc.
はこのように表すことができない。

これはまことに美しい定理であって，ガウスが平方剰余の相互法則を発見する最初のきっかけともなったものだ。残念なことに，どの証明もpが4n+1型の素数のときに，pを法として(-1)が平方剰余となることに基づいている。そして，その証明はそう簡単ではない。

投稿者 sukarabe : 07:39 | この記事の固定URI | コメント (4) | トラックバック (0)

2004年10月05日（火曜日）

何と，はてなダイアリーにmimeTeXが [ コンピュータ＆インターネット, 数学 ]

ふと思いついて，ラマヌジャンの検索をしたところ，はてなダイアリーのページが出てきた。そこから保型形式のページに行ったところ，数式が表示されている。どうやって表示しているのだろうか，とソースを見ると，なんとなんと，mimeTeX が使われている。そーか，はてなダイアリーには mimeTeX がインストールされているのかあ・・・。いやあ，驚いた。

投稿者 sukarabe : 17:17 | この記事の固定URI | コメント (0) | トラックバック (0)

2004年09月14日（火曜日）

ax+by [ 数学 ]

まったくの個人的な備忘録。a, bを互いに素な正の整数とすれば，整数x, yに対して，ax+byの形で表される数は整数全部になる。では，x, yとして自然数，つまり正の整数だけをとったときはどうなるだろうか。よく知られている(？)ように，ab+1 以上の整数はすべて表され，abは表すことができない。これは，平面上で直線 ax+by=c 上に格子点が等間隔にのっていることから分かる。では，abより小さい自然数はどうか。これは表されるものもあれば，そうでないものもある。完全な解答ではないが，Uspensky&Heaslet著 Elementary Number Theory の５９ページ以降，および６６ページに関連する話および練習問題を見つけた。ただし，x, yは正の整数ではなく，非負整数，つまり０以上の整数となっている。これは単に置き換えするだけで直ちに翻訳できる。

投稿者 sukarabe : 18:13 | この記事の固定URI | コメント (0) | トラックバック (0)

2004年08月23日（月曜日）

仕事 [ 数学 ]

初等幾何関係の原稿を書かなくてはならない。ずいぶん前から約束している仕事なのだが，いよいよ仕上げないとしゃれにならない状況だ。最初はしかたなく始めたのだが，これがなかなか楽しい。もっとも楽しいのは数学の事で，原稿を書くことになると楽しいわけじゃないが(苦笑)。問題として出題されると必ずしも楽しくないが，鑑賞するというつもりで色々読みあさると，初めて知ることを多く，初等幾何もなかなか素敵ではないか，と思う。だんだん知識が増え，よく使うテクニックが分かってくると，今度は逆に解説を読む前に自分で証明したくなるから不思議なものだ。しばらく考えて解けることもあるし，ギブアップして解説を読むこともある。それを続けていると，段々と解けるようになるからおもしろい。ああ，でもだいぶん進歩してしまったなあ。もう初心者じゃないかもしれない。行間が読めるようになってしまった。まずい(笑)。うーむ，初心者が原稿を書いた方が，丁寧で良い意味があるのだが・・・。

投稿者 sukarabe : 22:00 | この記事の固定URI | コメント (1) | トラックバック (0)